
 |
[2008 年 11 月号] |
[技術講座]
オブジェクトの広場 9 月号で「新・ソフトウェア開発の神話」[1]という書籍の紹介を行いましたが、その書籍の著者であるジョー・マラスコさんのセミナーを TPS ソフトウェア研究会様主催で 10/1 に名古屋、S-open 様主催で 10/2 に東京で開催しました。本記事では、そのセミナーで行ったマラスコさんの講演の概要と講演後の質疑の内容を 2, 3 回に渡って簡単に紹介したいと思います。
私は、大学で理系の教育を受け、物理学の研究者として道からソフトウェア開発の分野に移り、30 年間以上に渡りソフトウェア開発に関わる仕事を行ってきた。そのソフトウェア開発の仕事の中では、プログラマー、プロジェクトマネージャー、経営者を経験してきた。私が最も長く勤務したのはラショナルソフトウェア社だったが、その経歴の中では単にツールの開発を行ってきただけではなく、世界中の様々な業種のお客様でどのように開発を行っているかという点も学んできた。そのため、私の話はツールベンダーとしての特殊な世界だけではなく、ツールベンダー以外の企業でのソフトウェア開発にも通じるものだと考えている。私の経験をまとめたものが、「新・ソフトウェア開発の神話」という書籍である。
私の 30 年以上の経験を振り返って考えると、以下のような理由でソフトウェア開発はさらに難しくなっているといえる。
 |
それに伴い、このようなソフトウェア開発を管理するということもさらに難しくなっている。そのような困難な状況で、開発を成功させるためには、以下の 3 点が求められている。
ソフトウェア開発が他の分野と大きく異なるのは、以下の 2 点においてである。
今回の講演では、「新・ソフトウェア開発の神話」でも試みたように、ソフトウェア開発をあまり知らない人に、ソフトウェア開発の他の分野との違いを説明する方法を述べたいと思う。聞き手やテーマによって効果的なコミュニケーションのやり方が異なるため、「新・ソフトウェア開発の神話」では複数の説明方法を用いている。本講演では、それらの説明方法の中で以下の 3 つを取り上げる。
アナロジーは、説明したいことを聞き手がすでに知っている知識と結び付けて効果的に説明する方法である。アナロジーは強力だが、よいアナロジーであるためには以下の 2 つの条件を満たす必要がある。
これらの条件のうち前者を「対応付け条件」と呼び、後者を「通じる条件」と呼ぶ。
それでは、ここで以下のようなソフトウェア開発の原則を説明するアナロジーを考えてみよう。
1 は、作るべきソフトウェアにおいて既知で素性が分かった部分と未知でリスクが大きい部分をちゃんと見極めなければならないということである。2 は、計画は立案するものの、計画を実行する途上で学んだことにより、計画を適宜柔軟に見直していくべきであるということである。これら 1, 2の2 つの原則から、3, 4の原則が導き出される。
ここで反復的な開発を簡単に説明する。反復的な開発の特徴は、以下の 5 点にまとめられる。
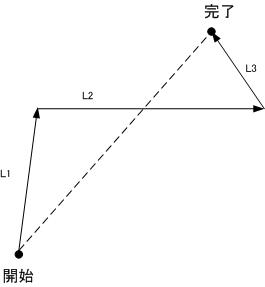 |
この反復的な開発の利点を図によって説明しよう。例えば、3 回の反復で開発を行う場合を図示すると図 1 のようになる。この図では、開発が理想的に行われた場合の軌跡を破線で表し、反復的な開発を行った場合の各反復の軌跡をベクトル(矢線)で表している。この図で、最初の反復のベクトルの終点では理想的な軌跡から大きく逸脱しているが、次の反復を表すベクトルで軌道を修正し、開発を進めている。2回目の反復を表すベクトルの終点も理想的な軌跡を通り越しているが、3 回目の反復で軌道修正をすることにより開発のゴールに到達することができる。
ウォーターフォール型開発の場合は、最初のベクトルの方向により長く進むことになるので、ゴールからさらに大きく逸れて大きな無駄が発生してしまうことになる。その結果、ウォーターフォール型開発は 3 回の反復を行う開発よりも効率が悪いものになる。
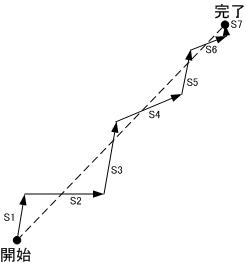
一方、7 回の反復で開発を行う場合を示したものが図 2 である。図 1 と比べて、各ベクトルの理想的な軌跡からの逸脱が少なくなり、3 回の反復で開発を行った場合よりもさらに無駄が少なくなっている。
ソフトウェア開発を管理するための原則として以下のようなものをさらに追加することができる。
 |
これらソフトウェア開発における 10 ケの原則を説明するためのアナロジーの候補として以下の 6 つのものを考えることができる。
これらのアナロジーの候補には良いものとイマイチなものがある。例えば、家を建てるというアナロジーの長所と短所は以下のとおりである。
この結果、短所として挙げられている点において「対応付け条件」が満たされないので、よいアナロジーとはいえないということになる。
これに対して、登山のアナロジーの長所と短所を考えると以下のようになる。
結局、「対応付け条件」は満たすが「通じる条件」を満たさないということにより、登山のアナロジーもよいアナロジーとはいえないということになる。但し、登山のアナロジーは柔軟な計画の見直し、チームワークなど反復的な開発やリスクターゲティングの要点をよく説明できるので、「新・ソフトウェア開発の神話」では 1 つの章を割いて説明を行っている。
この他、登山よりもさらによいアナロジーとして旅行やヨットなどについても講演で説明したが、本報告では割愛する。
アナロジーがどちらかといえば、「言葉」によるコミュニケーションを得意とする一般管理職や経営者に好まれるものである。それに対して、数学的なモデルは数字によるコミュニケーションを得意とする技術者に好まれるものである。
数学的モデルを用いる場合には、数学者であるリチャード・ハミングの「計算の目的は洞察を得ることであり、数字を得ることではない」という言葉に注意すべきである。そのため、数学的なモデルは以下のような繰り返しを通じて作るのがよい。
今回の講演では、フレデリック・ブルックスの法則を数学的なモデルの題材として用いる。ブルックスは、その著書である「人月の神話」[2]において「遅れているプロジェクトに要員を追加しても、さらに遅れるだけである」という有名な法則を記した。この法則は、その後様々なところで言及され、この法則が正しいということに合意するプロジェクトマネージャーは多いのではないかと思う。
私は、この法則をプロジェクト(または開発組織)に追加されたメンバー(新メンバー)が立ち上がるまでに発生する、以下の 2 つの効果が相乗したものだと考えている。
問題となるのは、これらの効果の影響が量的にどの程度であり、ブルックスの法則が常に成り立つかどうかという点である。
10 人の既存メンバーで 1 年の開発期間を要するプロジェクトに、5 人のメンバーを追加するという場合を考えてみよう。この場合には、これらの 2 つの効果は以下のようになる。
ここで、「有用な時間」とは既存のメンバーの生産性に換算した作業時間のことである。つまり、新メンバーでは分からないことやミスのために生産性が低下するので「有用な時間」が減り、その分からないことをフォローするために既存メンバーの「有用な時間」も減るということである。
結果的に、50% の要員を増員したのにも関わらず、実効的な戦力は 20% 増加したのにすぎないということである。50% の増員により、単純計算では開発期間を 33.3%( 4 ヶ月)短縮できるはずだが、実際には 16.6%( 2 ヶ月)短縮されるにすぎない。また、50% の増員により単位期間当たりの労務費は50%増加するので、全体の開発コストは 25% 増えることになる。さらに、増員後の開発生産性は増員前の 80% に低下する。
ここで、「有用な時間H」とブルックスの法則の原因となる 2 つの効果との関係を数学的なモデルで表現すると、以下のような式になる。
ここで、Hは既存メンバーだけで開発を行った場合の有用な時間を 1 として求めている。また、D は正確には「新メンバーの低い生産性で失われる有用な時間に対して既存メンバーが失う有用な時間の割合」である。この D を“足手まとい率”と呼ぶ。
さらに、メンバー追加後の組織全体の生産性 N は以下のように求めることができる。
講演では、「成長率 G 」と「乗数 M 」とを変化させた場合の N の値を等高線図でプロットした図や、G, D, M等のパラメータを変化させた場合の生産性への影響を作図して簡単に求めることができるノモグラフを紹介した。( 本報告ではこれらの図を割愛するが、興味のある方は「新・ソフトウェア開発の神話」の第 22 章をご参照ください。)これらの図から、「メンバーの追加により常にプロジェクトが遅れる」のではなく、「 P が低く、D が高い」という条件で起きることが分かる。
この数学的なモデルから以下のようなことが分かる。
D は、新メンバーが必要な知識を提供できる既存メンバーの数や、新メンバーが参考にできるドキュメントがどの程度整備されているかによって変わる。
プロジェクトへのメンバーの追加や開発組織の成長がどのような結果をもたらすかを予測するためには、自分の組織における P や D の値を把握することが大切である。また、常に自分が必要だと思うよりも多くの増員が必要だということを覚えておいた方がよい。
歴史的な事実(史実)は、アナロジーに似ている。但し、歴史的な事実がコミュニケーションで役立つためには、「歴史から学んだことは現在にも活かせる」と信じる必要がある。
歴史的な事実の利点には、以下のような点が挙げられる。
今回の講演で、史実として述べるのは 1628 年に進水したバーサ号というスウェーデン王立海軍の戦艦についてである。この戦艦は、進水後処女航海に出て 20 分で一陣の風を受けて傾き、50 名の乗組員を道づれにしてストックホルム港に沈んだ。この船の建造には、その当時のスウェーデンの GDP の 10% が費やされた。
この船の建造に際しては、以下のようなことが起きた。
これらのことが起きたのは、以下のような原因によるものだったと考えられる。
この事件が発生するのを、防げたのだろうか?以下のような理由で防げる可能性はあったと思われる。
この史実からソフトウェア開発のマネージャーが学べるのは以下のような点である。
本セミナーは講演に 1 時間 30 分、質疑に 30 分という時間配分で行いました。セミナー開催前は質疑の時間が余るのではないかと心配していましたが、それも杞憂に終わり、どこでも質疑に 30 分の枠を使い切りました。次回の記事では、頂いた様々な質疑の中で興味深かったものを記憶している範囲で紹介する予定です。
本セミナーの開催にご協力いただいた日本インフォメーションの深井社長様、名古屋工業大学の黒岩先生を始めとする TPS ソフトウェア研究会の皆様、S-openの皆様にこの場を借りて感謝致します。
| © 2008 OGIS-RI Co., Ltd. |
|