この連載記事は、最適化問題の1つである「組み合わせ最適化問題」を解くことのできる「OptaPlanner」を紹介します。連載第一回目の本記事では、組み合わせ最適化問題の例としてシフトスケジュール作成と集荷経路作成を題材にしながらOptaPlannerが組み合わせ最適化問題を解くために利用しているメタヒューリスティックな解法の概要説明と、適切にメタヒューリスティックな解法を動作させるためのポイントを説明したいと思います。
組み合わせ最適化とは
シフトスケジュール作成や巡回ルート作成などは組み合わせや順番を入れかえながらより良いパターンを試行錯誤しながら作っていくことが多いと思います。実際の業務では、シフトの作成の場合は休み希望日や保有スキルを加味しながらより負荷が均等な割当が必要となり、巡回ルート作成では拠点への到着・出発時間の制限を守りながらより効率的な拠点の周り方が必要となります。このような組み合わせや順番を様々に入れ替えより良いものを採択するという問題は、「組み合わせ問題」や「組み合わせ最適化」などと言われ、業務の改善を目指す場合に時折遭遇する問題です。
例えば、シフトスケジュールを作る場合を例にしてみましょう。

実際に業務としてシフトを作成する場合、上記のような休み希望日や保有するスキルを加味しながら負荷の均等化が必要となり、様々な割当を試しながら作ることとなります。シフトを割り当てる際に守る必要がある業務上のルール(以後「制約」と記述)がそれほど複雑ではない場合はシフト作成者の経験・技量で十分カバーでき、業務に支障のない時間で作成は可能です。しかし、メンバーが多い場合やより厳密な負荷の均等化が求められる場合は相当苦労されることが多いと思われます。
ですので、コンピュータの計算力を利用してシフトを作成しようとチャレンジされる場合もあるかもしれませんが、制約が複雑である場合は割り当て方法を明確にロジック化するのは非常に困難です。よって、もう一つの解き方として、コンピュータの計算力を利用して総当たりで割り当て方法を試し最も良さそうな割当を採択する、といった方法も考えられます。しかし、仮に10名に5日間のシフト(朝、昼、晩、休みの4種類)を割り当てる場合、すべてで410×5個の組み合わせが存在します。これは約13京の1兆倍(1.3*1030)パターンとなり、10000パターン/秒で計算しても400京年かかり太陽系の寿命が尽きるまで計算しても全く間に合いません。ですので、全パターンを計算して最も良いものを選ぶという戦略は現実的には不可能です。
そこで以前よりこのような膨大な組み合わせの中からより良い組み合わせを見つけ出すために様々手法が提案されており、実際に活用されている場面もあります。 OptaPlanner(https://www.optaplanner.org/)はそう言った取り組みの一つで、「メタヒューリスティックな解法」と分類されているいくつかのアルゴリズムをJavaにて実装し、「組み合わせ最適化」をより身近に使えるようにできる最適化エンジンです。
OptaPlannerとは
OptaPlannerはJBossコミュニティで作成されているプロダクトの一つで、Javaで作られたlightweightで組込み可能な最適化エンジンであると書かれています。元々は、drools solverやdrools plannerと言われていたもので、JBossコミュニティで作成されているBusiness Rules Management System(以下「BRMS」と記述)の「Drools」の一機能として作成されていたものです。Version 6より改名され「OptaPlanner」となっています。
BRMSでは「業務ルールに従い処理し、ある答えを出す」(とても単純化していますが)というものなので、OptaPlannerとの違いが分かりにくいと思われる場合もありますが、両者の最も大きな違いを理解すると使い分けがしやすくなります。その違いとは、OptaPlannerは「業務ルールに適合する膨大な組み合わせの中からより良いものを探し出す」ということに特化している点です。BRMSでもルールに従って組み合わせを作ることは可能ですが、いくつもの組み合わせの中からより良いものを探し出す点はあまり得意としません。OptaPlannerはいくつもの組み合わせの中からより良いものを探し出すことに特化した作りとなっています。
そのより良いものを探し出す方法として「メタヒューリスティックな解法」を実装しており、そこがBRMSには含まれない機能です。
メタヒューリスティックな解法とは
メタヒューリスティックな解法とは発見的法則もしくは経験則を指し、得られる解の精度に理論的な保証がない近似解法と言われ理論家からは避けられたりしますが、的を得て利用すると比較的短時間で解を出すこともでき、問題によってはほぼ唯一の選択肢となる場合もあります。
メタヒューリスティックが実際にどのようなことを行って答えを出すかは、実装されているアルゴリズムにより異なりますが、代表的なアルゴリズムの大まかな処理手順は以下となり、少しずつ組み合わせを変えながらより良い組み合わせを探索する、と言うのが基本コンセプトです。
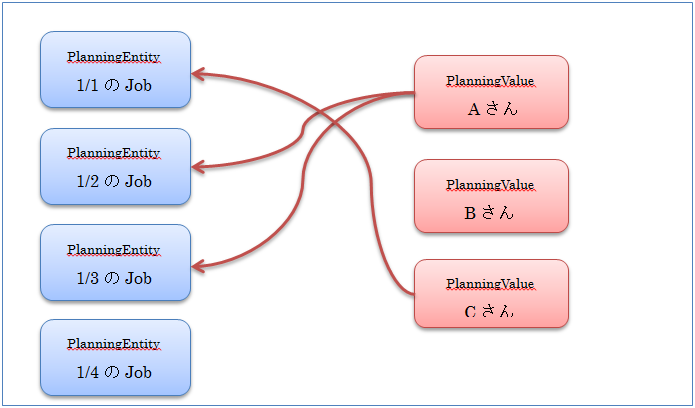
シフトスケジュールで割当を作成する場合を例に図示すると以下のようになります。
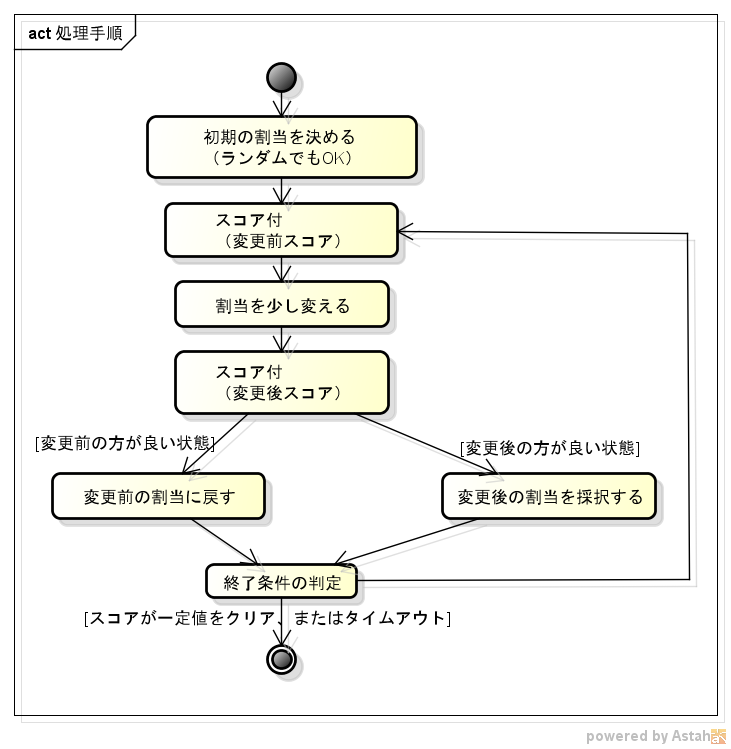
最初はランダムにでたらめな割当(シフトスケジュールの場合は業務ルールを無視して適当に人を割り当てた状態)、又は可能な限り適切な割当(最低限の休みやスキルは考慮し負荷平準化は簡素に、といった状態)を作成し、そこから組み合わせを少しずつ変更しながらより良い状態にしていきます。 その際、組み合わせを少し変更して変更前後で比較するため、作成した組み合わせの良し悪しを定量的に判断する必要があります。そこでルールに基づいて作成した組み合わせに対して「スコア付」という処理を行います。このスコアは業務上守るべき制約や負荷平準化の達成度などを基にしたものとなり、より良い組み合わせを探し出すためにとても重要なものとなります。(OptaPlannerでは、制約に違反した際に点数が加算されるモデルのため「ペナルティ値」との表現もされます)
「発見的法則もしくは経験則」と言うのは、この「少し変更して良いものを探索していく」と言う点です。「得られる解の精度に理論的な保証がない」と言うのも特徴的な点です。「割当を少し変更して」とあるように変更前と変更後を比較する際に変更しているのは、例えば10月1日のX業務に割り当たったAさんと10月10日のZ業務に割り当たったPさんを入れ替えてみた、といった小さな変更だけです。ですので、どうしても全割当パターンを比較するわけではないので、「最も良い状態」を確実に見つけられる保証がない、と言う点であると理解されておけば良いかと思います。
このメタヒューリスティックな解法は、アルゴリズム実装としては様々な改良・拡張が加えられたものが存在しており、問題の種類によってより適切なアルゴリズムを選択する必要が出てくる場合もあります。また、問題の種類によっては「メタヒューリスティックな解法」では解けないものも存在しますし、メタヒューリスティック以外のより適切な手法が存在する場合もあり、メタヒューリスティックは万能なアルゴリズムでは無い点も注意したいところです。
メタヒューリスティックな解法について、以下の書籍で詳しく解説されています。
組み合わせ問題をとらえる際のポイント
組み合わせ問題は「A(例:人)をB(例:仕事)に割り当てる」という形で表すことができます。 この場合、AとBの関係を「1:N」の関係で表すことができるとすると(ある人は複数の仕事に割り当て可能で、仕事には誰か一人を割り当てる)、OptaPlannerではA(例:人)をPlanningValue、B(例:仕事)をPlanningEntityと表現します。ですので、最適化問題をOptaPlannerで構築する際は、まず組み合わせ問題の「1:N」の関係をよく把握する必要があります。場合によって、「1:1」の関係もありますが、どちらかを「N」であると仮定し、業務上の制約条件で「1:1」になるように縛りを利かす方法があります。 また、解こうとする組み合わせ問題が「N:N」のような関係性の場合もあります。たとえば「各日には3名を割り当て、その際総コストを最小にしたい」という問題の場合、「人」と「日」をとらえると「N:N」の関係となります。しかし、OptaPlannerでは「N:N」の表現には対応していないため「1:N」の関係にする必要があります。そこで「日」の中には3つの「仕事」があり各仕事に誰かを割り当てる、と組み合わせ問題のとらえ方を変えると、人と仕事の関係を「1:N」で表すことができます。
この「1:N」の関係を把握して、何をPlanningValueにし、何をPlanningEntityにするかは対象とする問題によって変わるため、柔軟に考える必要もあります。例えば、同じシフトを組む問題でも人に対してシフトパターン(昼勤・夜勤・休み、など)を割り当てていく場合、シフトパターンをPlanningValue、人をPlanningEntityにする場合もあります。先ほどの例では同じ人をPlanningValueと扱っていましたが、問題の形が変わるとこのようにPlanningValueとPlanningEntityの役割を持たせる対象が変わる場合もあります。
OptaPlannerで開発する際のポイント
OptaPlannerでは、Javaクラスを利用して組み合わせ問題を表現します。前述にあるPlanningValueとPlanningEntityにあたるクラスと、組み合わせ問題全体をまとめるためのPlanningSolutionにあたるクラスを主要なものとして作成する必要があります。
実際に組み合わせを表現するにはPlanningEntityにはPlanningValueのプロパティ(getter,setter)を設け、PlanningEntityに対してPlanningValueを設定することで、組み合わせの表現を行います。例えば、PlanningEntityである「仕事」クラスのインスタンス「1月1日の仕事」に対して、PlanningValueである「人」クラスのインスタンス「Aさん」を設定する(関連付ける)、という感じになります。
| 用語 | 意味 |
|---|---|
| PlanningSolution | 最適化問題の全体を取りまとめるクラス。インスタンスを1つだけとなります。 |
| PlanningEntity | 上記の「N」にあたるもの。上記の例では「仕事」となり、インスタンスは複数存在します。 |
| PlanningValue | 上記の「1」にあたるもの。上記の例では「人」となり、インスタンスは複数存在します。 |
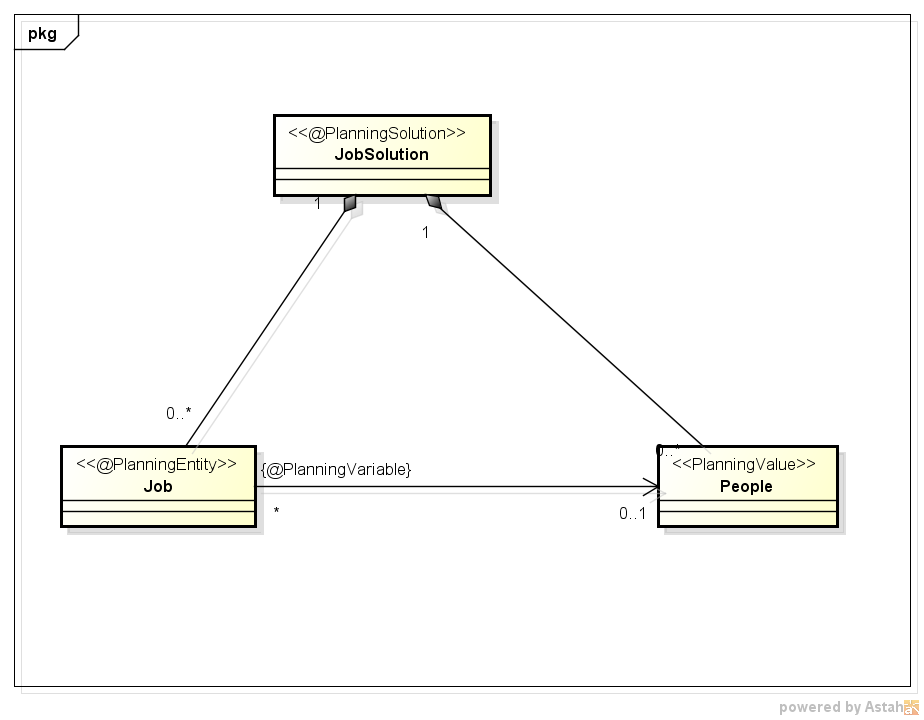
上図では、PlanningEntityである「Job(仕事)」は、PlanningValueである「People(人)」のプロパティを持ち、仕事と人の組み合わせの表現は「Job」インスタンスのプロパティに「People」インスタンスを設定するという形になります。実際にクラスをインスタンス化して組み合わせ問題を表示する際は、「1:N」の関係であるため以下のことも言えます。(設定によっては、上図のように「0..1:N」の関係も可能です)
- PlanningValueは複数のPlanningEntityに対して設定可能(Aさんは、1/2と1/3の仕事に割り当てられた、という場合)
- どのPlanningEntityにも割り当てられてないPlanningValueも存在可能(Bさんはどの仕事にも割り当てられていない)
- PlanningValueが設定されていないPlanningEntityも存在可能(1/4の仕事には誰も割り当てられていない)
より良い組み合わせを求める処理とは
組み合わせ問題をJavaで表現する方法が出来たので、実際に組み合わせ問題を解くにはどのようにしたら良いでしょうか。
この「組み合わせ問題を解く」と言う場合、業務上の様々な制約をクリアしている中で最も良い組み合わせを探したい、と言う場合が多く、そこで使われるのが前述にもある「メタヒューリスティックな解法」です。 このOptaPlannerが利用する「メタヒューリスティックな解法」とは、前述にもあるように「少しずつ組み合わせを変えながらより良い組み合わせを探索」と簡単にとらえることができます。(以後この組み合わせ問題を解く機能を「Solver」と記述)では、より良いシフトを探し出す際の簡単な例で見てみましょう。
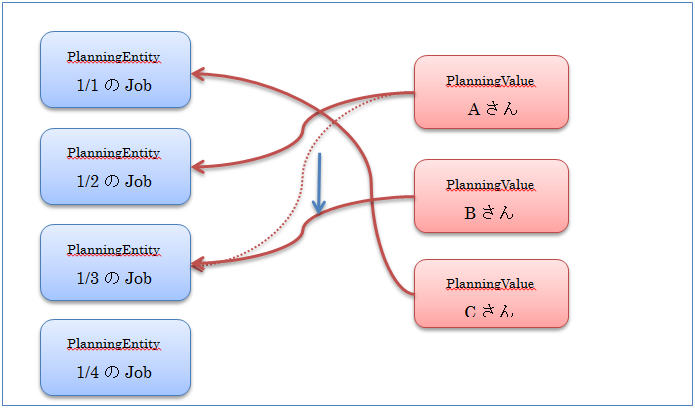
下記の例では、変更前は1月3日の仕事には「Aさん」を割り当てていましたが「Bさん」に変更し、この割当の変更前と後での「良さ」を比較し、変更後がより良い組み合わせであれば変更後の組み合わせを採択します。 OptaPlannerのSolverは、この「組み替え」と「前後の良さの比較」を繰り返し行い、徐々により良い組み合わせを探していきます。
この際に重要になるのが、組み合わせの良さを定量的に表現し、より良い組み合わせが変更前なのか変更後であるのかを判断する方法です。これをいかに適切に記述できるかが成功の可否に大きく影響します。
OptaPlannerでの「より良い組み合わせ」とは「いかに業務上課せられている制約に違反していないか」という視点になります。シフト作成では様々は制約が課せられており、例えば、「Aさんは1月3日は有給休暇を取得するので勤務できない」「1月3日の仕事には特殊なスキルが必要なのでBさんは担当できない」などといったものです。また、「Aさん、Bさん、Cさんの各担当回数には出来るだけ差がないようにしたい」といった負荷平準の制約も良くあります。 この「制約に違反した量を総計したスコア値」が「より良い組み合わせ」を判断する基準となり、OptaPlannerでは数値が大きいものを「より良い」と判断する設計となっています。ですので、組み合わせを改善していくと、スコア値はより大きな値となっていきます。
OptaPlannerでのスコア値の求め方のポイント
前述のようにOptaPlannerは数値が大きいものを「より良い」と判断する設計なので、制約に違反した量に「-1」をかけたものがスコア値として良く利用されます。これにより、前述の「より良い組み合わせ探索」を行うとスコア値は次第に「0」に近づいていき、制約に違反した量がより少なくなっていきます。(以後、スコア値に「-1」をかけたものを「ペナルティ値」と表現します)
このペナルティ値は最大で3つのカテゴリに分けて集計することも可能です。(それ以上分けることも可能ではありますが)このカテゴリは、業務上課せられている制約の重要性(絶対に守るべき制約や、出来れば守りたい制約、など)に対応するものです。
| カテゴリ | 概要 |
|---|---|
| Hard | 業務上課せられている制約が「絶対に守らなければならない」場合に利用します。 例:「Aさんは1月3日は有給休暇を取得するので、勤務できない」や、「1月3日の仕事には特殊なスキルが必要なので、Bさんは担当できない」 OptaPlannerのSolverによって作成された組み合わせで、「絶対に守らなければならない制約」が満たされていない場合に、このHardのペナルティ値を加算します。 Solverは、まずこのカテゴリのペナルティ値の総計が「0」になるように組み合わせを変更していきます。 |
| Midium | 業務上課せられている制約が「絶対に守らなければならない」が、条件次第ではどうしても満たすことができない場合もあり、その場は致し方なく制約を満たさない組み合わせを許容する、といった場合に利用するカテゴリです。 SolverはまずHardのペナルティ値を「0」にしてから、次にMediumのペナルティ値を「0」にします。 よって、条件次第では満たさなくてもよい(許容できる)制約についてはMediumを利用し、そのような制約が満たされていない場合はMediumのペナルティ値を加算します。 |
| Soft | 負荷平準化のように「出来るだけ制約を満たしたい」に場合に利用します。 各人の割当総回数の差ができるだけ小さくしたいが、様々な条件により差を「0」にすることができない場合があります。 また、トータルコストをできるだけ小さくしたい、利益をできるだけ大きくしたい、などの場合も利用されます。 |
このペナルティ値をどのような値から算出するかが的確により良い組み合わせを探索する際に重要となります。多くの場合は、「業務上課せられた制約からどれくらい離れているか」を定量的に表したものになりますが、アルゴリズムを正常に動かすにはいくつかの注意点があります。
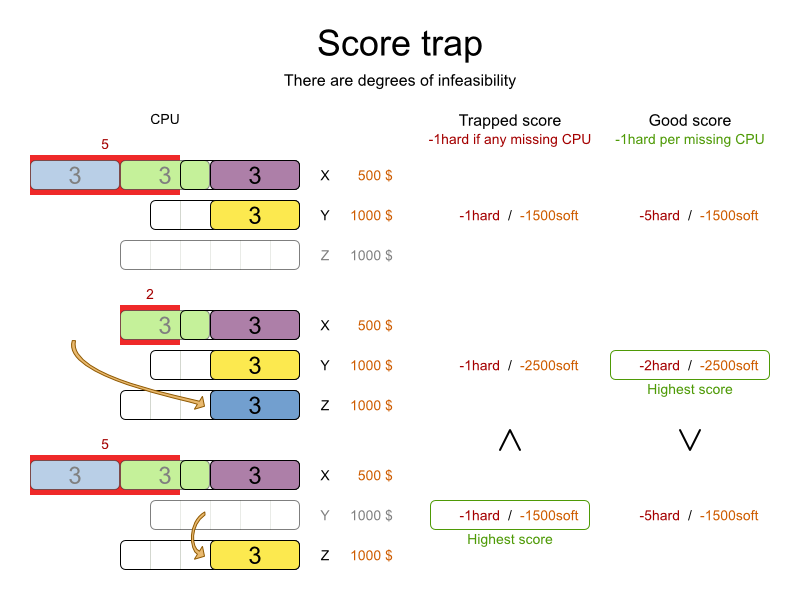
OptaPlannerのドキュメントにもある例を利用して説明したいと思います。上記はある一定容量までしか入れることのできない箱{X,Y,Z}に、様々な大きさを持った物を入れていく際、オーバーした容量をペナルティ値として加算するのがお勧めとなります。
より良い組み合わせが判断できなくなる誤った例として、「容量をオーバーした」という場合にだけ大きさ「-1」のペナルティ値を加算する、という「Trapped score」のような例があります。この誤ったペナルティ値の加算方法を行うと、Hardとしてカテゴリされている「容量をオーバーしない」という制約を「0」に近づけようとしますが、より「容量をオーバーしない」という制約を守っている2段目の組み合わせパターンと、他のパターンとの比較が適切に行えず、最悪の場合Hardとしてカテゴリされている「容量をオーバーしない」という制約を「0」にすることが出来なくなる場合があります。よって、組み替えの前後で「より良いものはどちらであるか?」「より違反量が少ないのはどちらか?」を判別できるようなペナルティ値になっているかがとても重要になります。
制約の種類によっては、「制約を満たしている」「制約を満たしていない」という判断しかできない場合もあります。例えば「ある仕事にある特定の人を割り当てた場合にその人はスキル不足で業務上課せられた制約を満たしていない」といった場合です。この場合は制約を満たしていない場合には「-1」のペナルティ値を加算する、という方法で問題ありません。作成中のシフトスケジュール全体を見た場合、スキル不足で本来割り当ててはいけない人に割り当たってしまっている、という箇所が一つずつでも減少すればいずれは全体としてより良い組み合わせを得ることができます。
まとめ
本記事は、シフトスケジュール作成を例に「組み合わせ最適化問題」とはどのようなものか、また、組み合わせ最適化問題を解くツールとしてJBoss Communityで開発されているOptaPlannerの紹介をし、OptaPlannerが採用しているメタヒューリスティクスという解法の概要説明と、どのように組み合わせ問題を捉え、より良い組み合わせをOptaPlannerで発見するポイントを示しました。
第二回目の次回は、OptaPlannerを使って実際にシフトスケジュールを作ってみたいと思います。