前回は弊社が技術開発した量子アニーリングによる献立提案を紹介しました。執筆後に弊社主催のフォーラムとD-Wave社主催のカンファレンスで講演もしていました。講演動画はこちらにありますので、ぜひご覧ください。さて、今回は実際に動かせるコードを元に技術面の深堀りをします。前回記事で撒いた伏線も回収していきます。未読の方は合わせてお読みいただければ幸いです。
1. はじめに
本記事では前回紹介した量子アニーリングによる献立提案をどのように実装するのか、そのエッセンスをまとめました。実際に動かせるPythonのコードを元に定式化の方法や結果の解釈を説明します。
組み合わせ最適化問題を解く手法としてアニーリングの定式化をまとめているサイトは色々ありますが、本記事は献立提案という目新しいテーマであるだけでなく、シンプルだけどあまり例を見ない方法で定式化しているという点でオリジナリティがあります。
また、最近は便利なライブラリの登場で頭を使わずにできてしまうことが多いですが、式変形や実装をすべて手動で行っている点も珍しいと思います。
「量子技術を使おう」というタイトルの連載ですが、使うだけでなく理解することを目指しています。量子技術はこれまでのコンピューティングと違って直感的に理解できることが少なく、ただ使ってるだけだと身につかないと感じています。連載を通して量子技術を使いこなせる人材が増えれば幸いです。
2. 実装の前に
前回の記事で量子アニーリングは“制約なし二値の二次計画問題"のみ解くことができると説明しました。式で書くと

が解けるということです。ここで、 xi, xj は量子ビットに対応していて、0 か 1 のいずれかを取る変数(以下、量子変数)です。式の最初にある min は、最小値を取る時の量子変数の値を求めるという意味です。
Qij はQUBO(Quadratic Unconstrained Binary Optimization)行列と呼ばれるもので、これが量子アニーリングの入力になります。
2.1. 目的項の式変形
ところで、前回の定式化で栄養バランスを考慮するための項(目的項)は
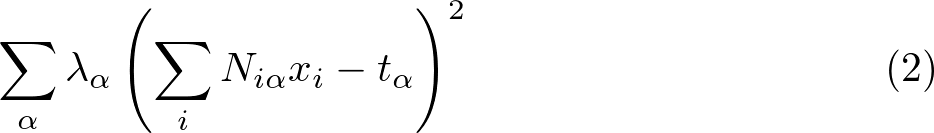
と書きました。各変数の説明は以下の通りです(前回記事から引用)。
ここで、量子変数 xi はレシピ i を使う場合は 1、使わない場合は 0 としています。Niα はレシピ i で摂取できる栄養素 α の値を表し、tα がその栄養素 α の目標値です。つまり、括弧の部分は「使われるレシピで摂取できる栄養素 α が目標値に近ければ小さい」ということを意味しています。
括弧の外の λα は栄養素 α をどれだけ重視するのかを表す変数です。個人の特性や状態に応じて柔軟に設計できる部分ですが、今回は簡単のため、重点的に摂取したい栄養素に対しては λ = 1、そうでなければ λ = 0 とします。
この式(2)をQUBO行列として実装できるよう式(1)の形に変形しておきます。
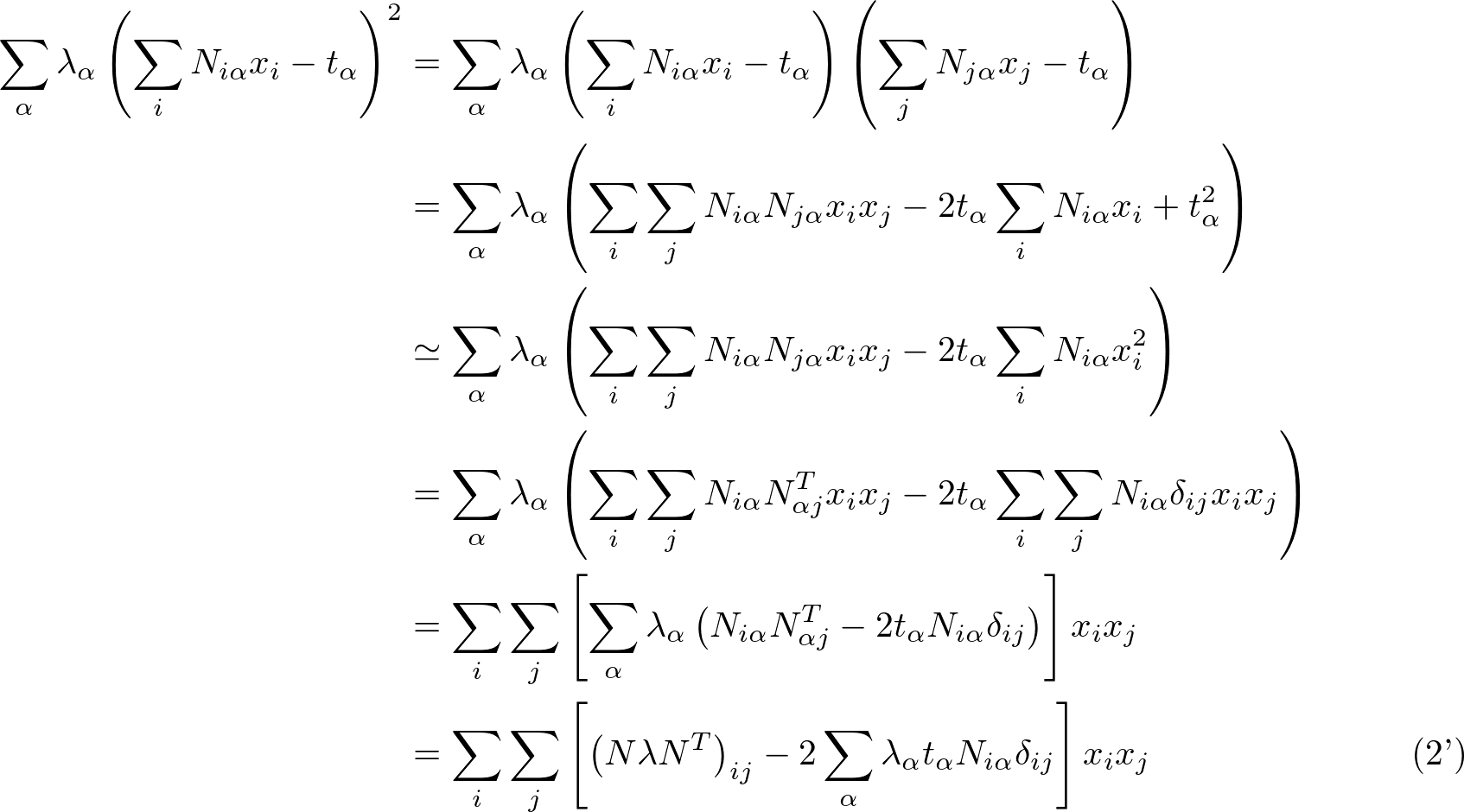
3段目の式変形では
- xi = xi2(xi = 0 or 1 なので2乗しても同じ値)
- 定数項 ti2 は省略(xi に依らないので式(1)の最小化で無視できる)
を使っています。
最後の式変形で1項目は α で和を取っていて、λ は λα を要素とした対角行列を表しています。和の計算を行列演算に置き換えるのは実装のためのテクニックです。
また、最後の式の [ と ] で囲まれた部分がQUBO行列(の一部)になります。添え字を見ると Qij の形になっているのが分かるかと思います。
実は、便利なライブラリを使えば最初の式を式変形することなくそのままQUBO行列に変換できます。しかし、本記事では定式化をすべて理解するという意図のもと、すべて自分で実装していきます。そこまで深追いする必要のない方はQUBO行列の実装箇所は飛ばしながら読み進めていただければと思います。
3. 献立提案の実装
以下ではGoogle Colaboratoryで実行することを想定して書いていきます。お手元のローカルPCでも実行できますが、Pythonの環境構築は適宜行ってください。
3.1. サンプルデータ作成
今回使うデータは、レシピ数100、栄養素5種類とし、栄養価は乱数で生成します。
import numpy as np import pandas as pd num_recipe = 100 # レシピ数 num_nut = 5 # 栄養素の種類数 np.random.seed(1) # 乱数種固定 df = pd.DataFrame(np.random.random((num_recipe, num_nut))) df.head() # 0 1 2 3 4 # 0 0.417022 0.720324 0.000114 0.302333 0.146756 # 1 0.092339 0.186260 0.345561 0.396767 0.538817 # 2 0.419195 0.685220 0.204452 0.878117 0.027388 # 3 0.670468 0.417305 0.558690 0.140387 0.198101 # 4 0.800745 0.968262 0.313424 0.692323 0.876389
今回はダミーデータなので、各栄養素の目標値は適当に以下のように設定します。
target = {
0: 1.2,
1: 1.4,
2: 1.6,
3: 1.8,
4: 2.0,
}
ここで、目標値が 1.0 になるように栄養素を規格化しておきます。
for key, val in target.items():
df[key] /= val
実際のデータだと、目標値が 1,000kcal くらいの摂取カロリー、せいぜい 1mg のビタミンB1のように単位も大きさもバラバラです。規格化しないと値が大きいほど最適化で重要視されることになるので、相対値で扱っても問題ない場合は規格化して使うことをオススメします。
次に、レシピを主菜、副菜、汁物に分けます。
num_type = 3 # レシピを[主菜、副菜、汁物]の3つに分類
df['MealType'] = np.random.randint(0, num_type, num_recipe)
df = df.sort_values('MealType').reset_index(drop=True)
df
# 0 1 2 3 4 MealType
# 0 0.347518 0.514517 0.000071 0.167963 0.073378 0
# 1 0.143617 0.097954 0.582872 0.387121 0.033000 0
# 2 0.629553 0.538483 0.576890 0.395292 0.062135 0
# 3 0.641866 0.522663 0.162311 0.142816 0.316152 0
# 4 0.542754 0.502512 0.381401 0.444231 0.017286 0
# ... ... ... ... ... ... ...
# 95 0.530504 0.709938 0.341294 0.292459 0.067714 2
# 96 0.197522 0.645271 0.358550 0.001595 0.308572 2
# 97 0.095622 0.678207 0.281195 0.321328 0.204068 2
# 98 0.199873 0.352693 0.387472 0.460545 0.078396 2
# 99 0.510026 0.038507 0.262621 0.377260 0.459301 2
MealType という列を追加しており、0 は主菜、1 は副菜、2 は汁物に対応していると考えます。このあとの可視化で見やすいように MealType の昇順でソートもしています。
それでは、このデータを使って献立提案をしてみましょう。主菜、副菜、汁物が1つずつ選ばれていれば成功とします。
3.2. QUBO行列作成(目的項のみ)
はじめに、QUBO行列のメインとなる目的項を実装します。
目的項は前章で以下のように書き換えてました。
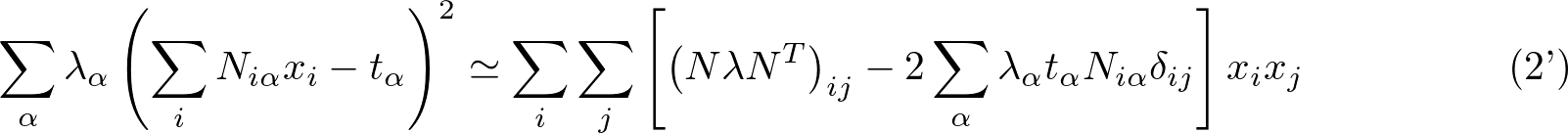
この [ と ] で囲まれた部分がQUBO行列でしたね。これをそのまま実装すると以下のようになります。
N = df[range(num_nut)].values
lam = [1.0] * num_nut # 簡単のため重要度λαは全て1.0で固定
q1 = N @ np.diag(lam) @ N.T # 式(2')の1項目
for i in range(num_recipe):
nut_sum = 0
for alpha in range(num_nut):
nut_sum += 2 * lam[alpha] * N[i,alpha] # 目標値tαは1.0に規格化済みのため略
q1[i,i] -= nut_sum # 式(2')の2項目
どのような行列になっているのかヒートマップで可視化して確認してみます。
# 可視化ライブラリseabornを使用 import seaborn as sns sns.heatmap(q1, center=0)
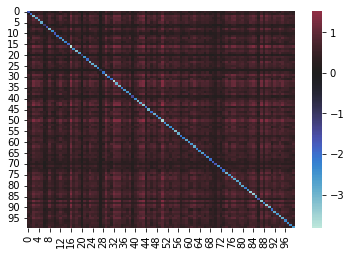
対角成分が青(負の値)で非対角成分が赤(正の値)になっていますね。
ここで、QUBO行列と最適化の関係を補足しておきます。
量子変数 xi は 0 か 1 を取る変数でしたが、1 を取る場合はその i 番目のレシピを献立に使うという意味です。xi が 1 を取ると、QUBO行列の i 番目の対角成分(上のコードで言うと q1[i,i])がコストとして足されます。最適化計算ではこのコストを最小化させる xi の値を求めることになります。
上の行列だと対角成分は負の値になっているため、足していくとコストはどんどん小さくなります。そのため、対角成分だけ考えるとすべての xi が 1、つまり、全レシピを使うことが最適(最小)です。しかし、そうすると食べ過ぎて栄養素を目標より摂り過ぎてしまうことになります。
そうならないように非対角成分が正の値で存在しています。xi と xj が共に 1 の場合は、行列の (i, j) 成分(q1[i,j])と (j, i) 成分(q1[j,i])がコストとして足されます1。このコストが xi と xj はどちらかのみ 1、もしくはどちらも 0 の方が最適(最小)としてくれます。
まとめると、対角成分と非対角成分のバランスによって栄養素を目標通り摂取できるようなレシピ組み合わせを求めることができます。
SA実行(目的項のみ)
まだ制約項を入れてないですが、これをQUBO行列としてシミュレーテッドアニーリング(SA)を実行してみましょう。
SAを実行するためにD-Wave社が開発しているOcean SDKというライブラリを導入します(ドキュメントはこちら)。
!pip install dwave-ocean-sdk
SAは以下のように数行で実行できます(以下、このあと複数回実行するものは関数化しています)。
import neal
def run_sa(qubo, num_reads=1000):
sampler = neal.SimulatedAnnealingSampler()
response = sampler.sample_qubo(qubo, num_reads=num_reads)
return response
SAのサンプリング数(試行回数)は num_reads で設定しており、大きくするほど精度が良くなりますが、時間も掛かります。今回の100レシピの組み合わせ最適化だと1,000試行は10秒未満で終わります。
それでは、実行してみます。
QUBO = q1
response = run_sa(QUBO)
response.first
# Sample(sample={0: 0, 1: 1, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0, 7: 0, 8: 0, 9: 0, 10: 0, 11: 0, 12: 0, 13: 0, 14: 0, 15: 0, 16: 0, 17: 0, 18: 0, 19: 0, 20: 0, 21: 0, 22: 0, 23: 0, 24: 0, 25: 0, 26: 0, 27: 1, 28: 0, 29: 1, 30: 0, 31: 0, 32: 0, 33: 0, 34: 0, 35: 0, 36: 0, 37: 0, 38: 0, 39: 0, 40: 0, 41: 0, 42: 0, 43: 0, 44: 0, 45: 0, 46: 0, 47: 0, 48: 0, 49: 0, 50: 0, 51: 0, 52: 0, 53: 0, 54: 0, 55: 0, 56: 0, 57: 0, 58: 0, 59: 0, 60: 0, 61: 0, 62: 0, 63: 0, 64: 0, 65: 0, 66: 0, 67: 0, 68: 0, 69: 0, 70: 1, 71: 0, 72: 0, 73: 0, 74: 0, 75: 0, 76: 0, 77: 0, 78: 0, 79: 0, 80: 0, 81: 0, 82: 0, 83: 0, 84: 0, 85: 0, 86: 0, 87: 0, 88: 0, 89: 0, 90: 0, 91: 0, 92: 0, 93: 0, 94: 0, 95: 0, 96: 0, 97: 0, 98: 0, 99: 0}, energy=-4.997688106409669, num_occurrences=1)
最後の response.first で最良解2を表示しています。SAの実行時乱数のせいで結果はばらつきますが、参考に私の手元で得られた結果を載せています(上記コメントアウトした部分)。
この結果から最も目標値に近い栄養が摂れるレシピの組み合わせとして提案されたものを取り出します。
def get_optimal_combination(_df, response):
df = _df.copy() # 元データの上書き防止
df['Result'] = response.first.sample.values()
optimal_combination = df[df.Result==1]
return optimal_combination
optimal_recipes = get_optimal_combination(df, response)
optimal_recipes
# 0 1 2 3 4 MealType Result
# 1 0.143617 0.097954 0.582872 0.387121 0.033000 0 1
# 27 0.119519 0.055991 0.011458 0.037069 0.229292 0 1
# 29 0.667287 0.691615 0.195890 0.384624 0.438195 0 1
# 70 0.076949 0.133043 0.215975 0.220426 0.269408 2 1
今は制約を課さずに実行したので MealType を見ると、0(主菜)が3つで、1(副菜)がないです。つまり、献立提案としては失敗しています。
最良解以外で成功したものがあるのか、サンプリングして得られた1,000個の解がそれぞれいくつのレシピを使っているのか数えてみます。
from collections import defaultdict
def count_recipe_num(response):
counts = defaultdict(int)
for rec in response.record:
result = rec[0]
counts[len(result[result==1])] += 1
return sorted(counts.items())
count_recipe_num(response)
# [(3, 123), (4, 610), (5, 256), (6, 11)]
返り値のリストは
- 3つのレシピを使う献立が 123 個
- 4つのレシピを使う献立が 610 個
- 5つのレシピを使う献立が 256 個
- 6つのレシピを使う献立が 11 個
だったことを表しています。
4つ以上のレシピを使う献立が9割近く占め、制約なしでは献立提案がうまくできないことが分かります。
一方で、各栄養素の摂取率を見ると
def total_nut(optimal_recipes, num=num_nut): return optimal_recipes[range(num)].sum() total_nut(optimal_recipes) # 0 1.007372 # 1 0.978603 # 2 1.006196 # 3 1.029241 # 4 0.969895
誤差 ±3%(1.0で100%)で概ね目標通りになっています。
最後に、目標からの乖離度として式(2)を計算します。
def calc_diff(optimal_recipes, num=num_nut):
return ((optimal_recipes[range(num)].sum() - 1)**2).sum()
calc_diff(optimal_recipes)
# 0.0023118935909176414
この値は他の手法で最適化した時に比較対象となる指標です。どの最適化アルゴリズムが適しているのかは、こういった精度指標と計算時間を元に判断することになります。
3.3. QUBO行列作成(制約項追加)
献立提案を妥当なものにするために制約を課しましょう。
前回の記事で制約項は以下の形と紹介しました。

ここで、Cij はレシピ i とレシピ j の献立区分が同じであれば 1、異なっていれば 0 となる行列です。ただし、i = j の対角要素は 0 とします。
この項は one-hot encoding というテクニックを使うと、行列演算で実装できます。
p = pd.get_dummies(df['MealType'], dtype=float).values # one-hot encoding q2 = p @ p.T q2 -= np.identity(len(q2)) # 対角成分を 0 にする
制約項もどんな行列か可視化して確認します。
sns.heatmap(q2, center=0)
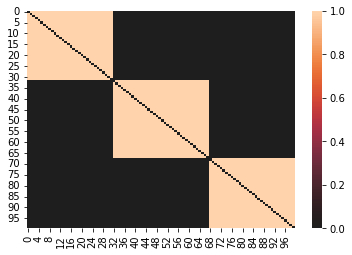
データ作成時に MealType でソートしていたので、上から主菜、副菜、汁物のレシピがブロック状に並んでいます。明るいところの値が 1 で、ほかは 0 です。
この行列をQUBO行列に加えた場合、同じ献立区分のものが同時に選ばれるとコストが 1 掛かります。つまり、主菜、副菜、汁物がそれぞれ複数個選ばれないよう抑止力が働きます。
SA実行(制約項追加)
この制約項をQUBO行列に加えてSAを実行してみましょう。コードはほぼ先ほどと同じです。
QUBO = q1 + q2 # ここだけ変更
response = run_sa(QUBO)
response.first
# Sample(sample={0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0, 7: 0, 8: 0, 9: 0, 10: 0, 11: 0, 12: 0, 13: 0, 14: 0, 15: 0, 16: 0, 17: 0, 18: 0, 19: 0, 20: 0, 21: 0, 22: 0, 23: 0, 24: 0, 25: 1, 26: 0, 27: 0, 28: 0, 29: 0, 30: 0, 31: 0, 32: 0, 33: 0, 34: 0, 35: 0, 36: 0, 37: 0, 38: 0, 39: 0, 40: 0, 41: 0, 42: 0, 43: 0, 44: 1, 45: 0, 46: 0, 47: 0, 48: 0, 49: 0, 50: 0, 51: 0, 52: 0, 53: 0, 54: 0, 55: 0, 56: 0, 57: 0, 58: 0, 59: 0, 60: 0, 61: 0, 62: 0, 63: 0, 64: 0, 65: 0, 66: 0, 67: 0, 68: 0, 69: 0, 70: 0, 71: 0, 72: 0, 73: 0, 74: 0, 75: 0, 76: 1, 77: 0, 78: 0, 79: 0, 80: 0, 81: 0, 82: 0, 83: 0, 84: 0, 85: 0, 86: 0, 87: 0, 88: 0, 89: 0, 90: 0, 91: 0, 92: 0, 93: 0, 94: 0, 95: 0, 96: 0, 97: 0, 98: 0, 99: 0}, energy=-4.997421280524122, num_occurrences=1)
最良解は以下の組み合わせになりました。
optimal_recipes = get_optimal_combination(df, response) optimal_recipes # 0 1 2 3 4 MealType Result # 25 0.090849 0.452705 0.501852 0.387111 0.383106 0 1 # 44 0.094452 0.019845 0.471788 0.219361 0.373469 1 1 # 76 0.799529 0.574258 0.020202 0.394104 0.232501 2 1
目的項だけの結果と違い、今回は MealType が異なるレシピ3つの組み合わせになっています。つまり、これで期待していた献立(主菜、副菜、汁物の組み合わせ)が提案できたことになります。
栄養素の摂取率は
total_nut(optimal_recipes) # 0 0.984829 # 1 1.046808 # 2 0.993842 # 3 1.000577 # 4 0.989076
で、98%~105% でした。目的項だけで求めた最良解と比べると、目標値とのズレが少し大きくなりました。
一般に、制約があると目標への到達度は下がります。制約が多く条件が厳しければ大きく下がることもあり、最良解であっても役に立たない結果にもなり得ます。今回だと、制約は満たすけど全部の栄養素が50%程度しか摂れないという結果になると、わざわざ最適化したメリットを感じませんよね。
そこで、組み合わせ最適化問題は定式化して結果を求めるだけでなく、その結果がどれだけ目標に近いのかも忘れずにチェックする必要があります。 得られた最適解が目標から遠すぎるのであれば、目標や制約を見直すだけでなく、問題設定から再検討する必要があるかもしれません。
最後に、目標からの乖離度は以下の通りです。
calc_diff(optimal_recipes) # 0.0025787194751868076
3.4. QUBO行列作成(罰金項に変更)
ところで、先ほどの結果で1,000回試行したうち6回は、3つではなく2つのレシピ組み合わせでした。
count_recipe_num(response) # [(2, 6), (3, 994)]
実際の献立でも主菜が豪華だから副菜or汁物はいらないということはあると思います。上記の制約項(式(3))はそういった組み合わせを許容するように定式化しています。
一方で、罰金項と呼ばれる定式化もあります。前回の記事では以下のように紹介していました。

ここで、Piβ はレシピ i の献立区分を表す行列で、β が献立区分に対応しています。括弧中の和は選ばれたレシピの中で同じ献立区分のものが何個入っているかを表していて、式全体では「主菜・副菜・汁物が1つずつ選ばれると 0、そうでなければより大きい」ことを表しています。
この項も実装してみましょう。展開すると以下のようになります。
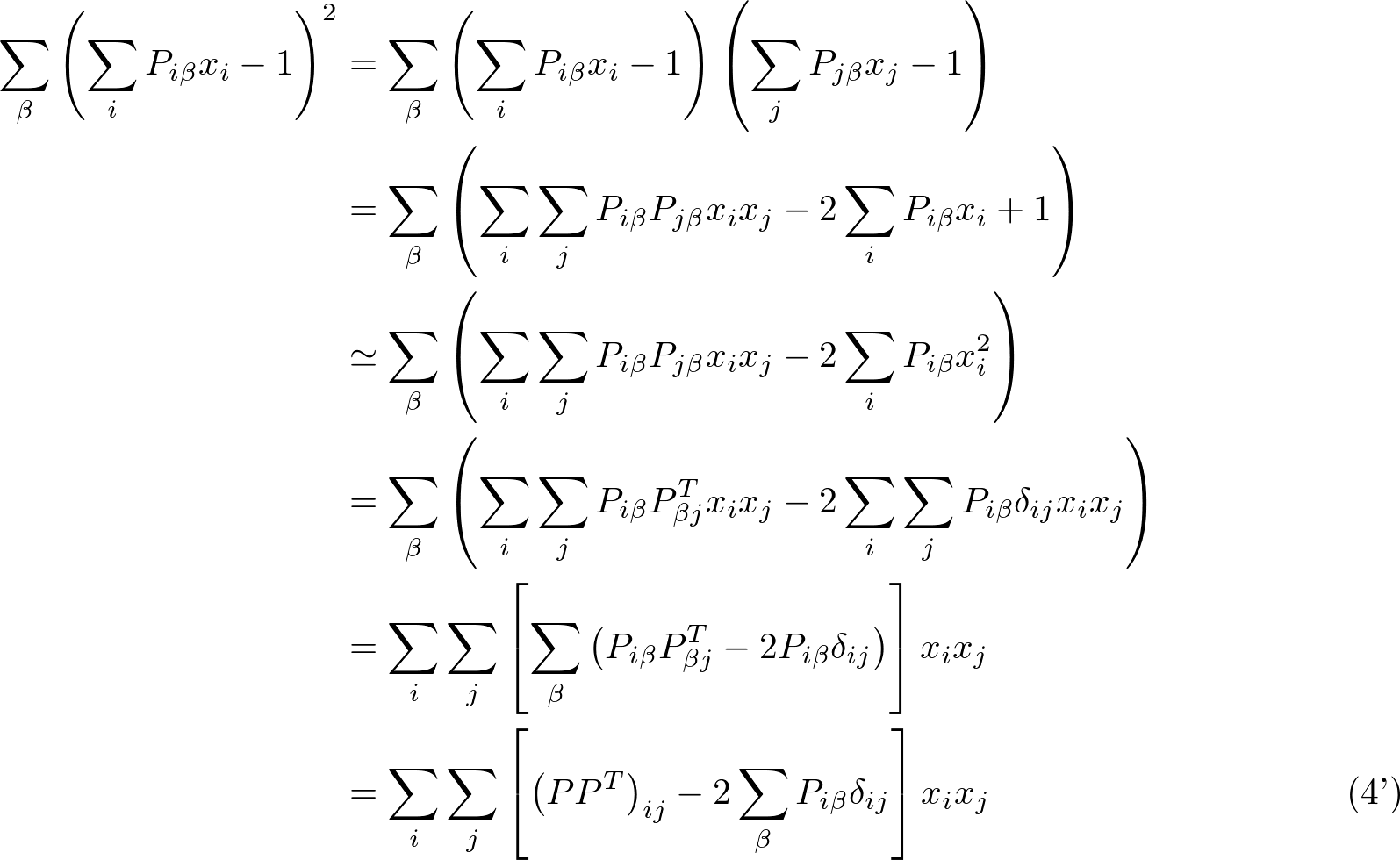
最後の式で2項目の和は条件次第で簡単に計算できます。今回は各レシピが主菜、副菜、汁物のいずれかであるため、レシピ i に依らず Σβ Piβ = 1 になります。
この実装は素直に以下のように書けます。
p = pd.get_dummies(df['MealType'], dtype=float).values # one-hot encoding q3 = p @ p.T q3 -= 2 * np.identity(len(q3)) # ここだけ q2 の計算と異なる
実は制約項で one-hot encoding していたのは式(4)における行列 Piβ を作っていたのでした。制約項の実装と見比べると、違いは最後の引き算を2倍しているところだけです。
この行列も可視化して確認してみます。
sns.heatmap(q3, center=0)
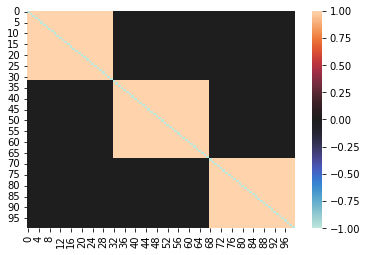
制約項の時は対角成分がすべて 0 でしたが、罰金項の場合は -1 になっています。
SA実行(罰金項に変更)
それでは、制約項を罰金項に置き換えてSAを実行してみましょう。
QUBO = q1 + q3 # ここだけ変更
response = run_sa(QUBO)
response.first
# Sample(sample={0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0, 7: 0, 8: 0, 9: 0, 10: 0, 11: 0, 12: 0, 13: 0, 14: 0, 15: 0, 16: 0, 17: 1, 18: 0, 19: 0, 20: 0, 21: 0, 22: 0, 23: 0, 24: 0, 25: 0, 26: 0, 27: 0, 28: 0, 29: 0, 30: 0, 31: 0, 32: 0, 33: 0, 34: 0, 35: 0, 36: 0, 37: 1, 38: 0, 39: 0, 40: 0, 41: 0, 42: 0, 43: 0, 44: 0, 45: 0, 46: 0, 47: 0, 48: 0, 49: 0, 50: 0, 51: 0, 52: 0, 53: 0, 54: 0, 55: 0, 56: 0, 57: 0, 58: 0, 59: 0, 60: 0, 61: 0, 62: 0, 63: 0, 64: 0, 65: 0, 66: 0, 67: 0, 68: 0, 69: 0, 70: 0, 71: 0, 72: 0, 73: 0, 74: 0, 75: 0, 76: 0, 77: 0, 78: 0, 79: 0, 80: 0, 81: 0, 82: 0, 83: 1, 84: 0, 85: 0, 86: 0, 87: 0, 88: 0, 89: 0, 90: 0, 91: 0, 92: 0, 93: 0, 94: 0, 95: 0, 96: 0, 97: 0, 98: 0, 99: 0}, energy=-7.9933891482037325, num_occurrences=1)
最良解は以下のようになりました。
optimal_recipes = get_optimal_combination(df, response) optimal_recipes # 0 1 2 3 4 MealType Result # 17 0.268901 0.479135 0.281796 0.212279 0.205406 0 1 # 37 0.397617 0.109051 0.388629 0.302228 0.327069 1 1 # 83 0.404992 0.431650 0.343467 0.514545 0.459367 2 1
また、すべての解が3つのレシピ組み合わせになっていることも確認できます。
count_recipe_num(response) # [(3, 1000)]
最後に、最良解の栄養素摂取率は
total_nut(optimal_recipes) # 0 1.071511 # 1 1.019836 # 2 1.013893 # 3 1.029052 # 4 0.991841
で、目標からの乖離度は以下の通りです。
calc_diff(optimal_recipes) # 0.006610851789942001
制約項の最良解より乖離度が大きくなってますが、run_sa() 関数を何度も実行すれば(もしくは試行回数 num_reads を大きくすれば)同じ結果が出たりより良い解が出たりします。SAはヒューリスティックな手法がゆえに精度の保証はできません。とはいえ、献立提案のように厳密解でなくとも許容できる用途には、高速に解が求められるので十分役に立ちます。
補足:なぜ制約項と罰金項が似ているのか
制約項と罰金項はそれぞれ式(3)と式(4)で全然違うものに見えますが、なぜこれほど似ているのでしょうか?偶然なのか意味があるのか気になる方もいらっしゃるかと思います。
実は制約項は罰金項と同じ形に書き換えられます。式変形は罰金項の展開と逆向きに辿るだけなので省略しますが、以下のように書き換えられます。
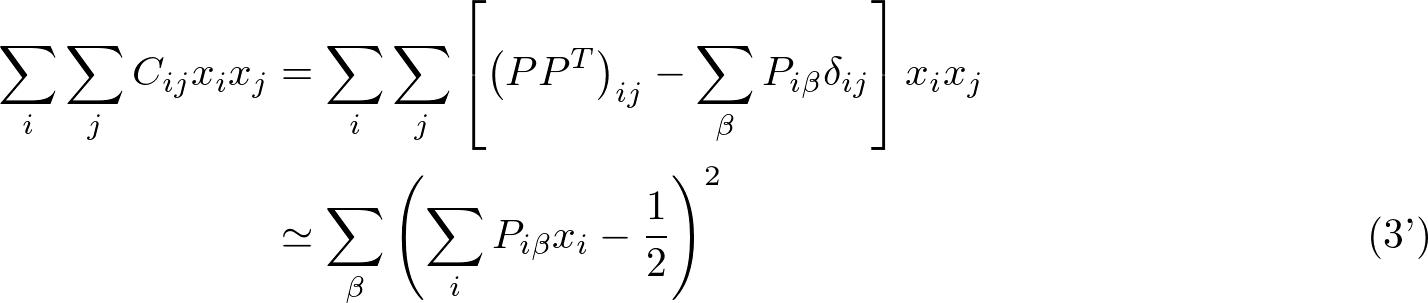
つまり、罰金項(式(4))の 1 が ½ に置き換わった式になっています。
この式を罰金項のように解釈してみると、主菜、副菜、汁物の数が ½ ずつだったら最適ということになります。しかし、レシピの数は整数値ですので、主菜、副菜、汁物の数が 0 でも 1 でも違いがないと捉えることができます。この柔軟さが「主菜が豪華だから副菜or汁物はなしでもOK」という結果を導きます。
また、この式は量子アニーリングにおける最適化計算にもメリットがあります。ここで述べるには専門的になりすぎるため、興味のある方は大関教授の講義動画をご参照ください(該当箇所は3:16:24~)。この動画以外にも大関教授の動画は参考になるものが多く、量子アニーリングの実用化を目指す場合はすべて必聴に感じます。ただし、大学の講義1単位取るくらいの時間が掛かります^^;
3.5. 制約条件の追加
実際の献立提案ではレシピの数だけでなく、考慮すべきことがたくさんあります。たとえば
- 和洋中などの料理ジャンルが統一されている
- 調理時間の長いレシピは最大1つ
- メインとなる食材が被らない
といったことが挙げられます。また、
- 特定の材料を使いたい
- レシピ1つは決めたから付け合わせを提案して欲しい
などユーザから指定したいこともありそうです。
我々の技術開発では、上記のような条件も実装しています。「特定の材料を使いたい」けど「メインとなる食材が被らない」という条件は工夫が必要ですが、どの条件も上述の制約項と同じ形で定式化できます。
実際の献立提案の様子はD-Wave社主催のQubitsでの講演でデモをしたので、興味のある方はそちらもご覧ください(デモは12:55~)。
4. 量子アニーリングの実行
お待たせしました。ここでやっと量子アニーリング(QA)が出てきます。
QAは基本有料のサービスですが、執筆時点(2023年4月)ではD-Wave Leapの個人アカウントを新規作成すると無料枠があります。今回の問題を試すくらいの枠はあるので、実際に動かしてみることも可能です。
4.1. 純粋なQAを実行する場合
純粋なQAの実行は前章で実装したSAとほぼ同じです("純粋な"というのはこのあと紹介するハイブリッドソルバーと混同しないように付けてます)。
from dwave.system import DWaveSampler, EmbeddingComposite
TOKEN = "" # TODO: 自分のトークンを設定
ENDPOINT = "" # TODO: 接続先(リージョン)を設定
def run_qa(qubo, num_reads=1000):
sampler = EmbeddingComposite(
DWaveSampler(token=TOKEN, endpoint=ENDPOINT,
solver='Advantage_system4.1')
)
response = sampler.sample_qubo(qubo, num_reads=num_reads)
return response
ここで、実行時の注意点がいくつかあります。
- トークンとエンドポイントを設定する
EmbeddingComposite()に時間が掛かるsolverに指定できる文字列は随時更新されるsampler.sample_qubo()の実行は一瞬だが計算が終わるタイミングは別
1)公式ドキュメントを参考に TOKEN と ENDPOINT に適切な文字列を入れてご使用ください。
2)量子アニーリングマシンという実機を動かす際に、QUBO行列を物理的にどう表現するのか決める必要があります。それを"埋め込み"と呼びますが、その計算自体が組み合わせ最適化問題を解くことに相当しており、手元の実行環境で計算されます。そのため、問題サイズが大きいとQAの実行前に分単位で時間が掛かります。
3)DWaveSampler() の引数 solver は利用する実機を指定する文字列です。使える実機はアップデートされると増えたり、減ったり(名称変更したり)するので要注意です。契約形態によっても変わると思います。詳細は上述の公式ドキュメントをご参照ください。
4)API的には sampler.sample_qubo() は実行したらすぐに終わります。しかし、実機のあるカナダへのデータ転送やQAの実行など諸々時間が掛かります。そのため、結果を取得するタイミング(たとえば response.first の呼び出し時)にそういったことが全部終わるまで待つ必要があります。
4.2. ハイブリッドソルバーを実行する場合
古典計算も交えたハイブリッドソルバーを使う場合は、作成済みのQUBO行列を変換して使います(ライブラリで提供されている機能を用いてQUBO行列を作成する方が一般的かもしれません)。
from dwave.system import LeapHybridSampler, LeapHybridCQMSampler
import dimod
def run_bqm(qubo):
sampler = LeapHybridSampler(token=TOKEN, endpoint=ENDPOINT,
solver='hybrid_binary_quadratic_model_version2')
qubo_bqm = dimod.BQM.from_qubo(qubo)
response = sampler.sample(qubo_bqm)
return response
def run_cqm(qubo):
sampler = LeapHybridCQMSampler(token=TOKEN, endpoint=ENDPOINT,
solver='hybrid_constrained_quadratic_model_version1')
qubo_bqm = dimod.BQM.from_qubo(qubo)
qubo_cqm = dimod.CQM.from_bqm(qubo_bqm)
response = sampler.sample_cqm(qubo_cqm)
return response
ハイブリッドソルバーはすべてD-Wave社の環境で実行され、手元の環境で埋め込み計算もされません。そのため、上記の関数は一瞬で終わります。
ただし、前節の注意点4で述べたように計算結果の取得には時間が掛かります。とくに、ハイブリッドソルバーは実行関数 LeapHybridSampler.sample() と LeapHybridCQMSampler.sample_cqm() が time_limit という引数を持っていて、最低でもその時間は掛かります(私が検証していた2022年時点の time_limit は、BQMは3秒、CQMは5秒でした)。
4.3. 実行結果
純粋なQAではまともな結果が得られませんでした。まともでないというのは一所懸命実装した制約条件を全然満たしてくれないという意味です。
具体的には以下のような結果になりました(ムダ打ちになることが分かっていたので num_reads=100 に減らしてます)。
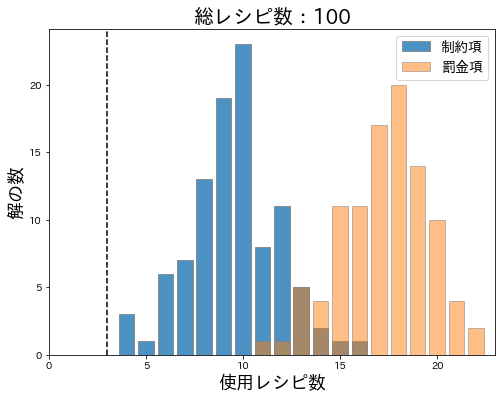
横軸は献立として得られた解が何個のレシピを使っているかで、縦軸が頻度を表しています。黒の点線が今回期待している3個の位置ですが、すべて4個以上のレシピを使う献立になっています。つまり、どの解も役に立ちません。
これは非常に残念なことですが、SAと同じ定式化でそのままQAを実行すると大抵このような結果になります。とくに、罰金項の方が制約項より使用レシピ数が多くなっていて、より条件から外れています。
そのため、(現時点での)量子アニーリングマシンは罰金項で定式化される典型的な問題である巡回セールスマン問題が苦手です。ただ、色々と工夫をすればその限りではなく解けないと言い切ってしまうのは語弊があります。工夫の方法は株式会社Fixstars Amplifyさんがデモコード付きで紹介されています。他にも多くの解説記事があり、専門的なことも丁寧に説明されていて非常に参考になります。
次に、どの程度レシピ総数を減らせば解けるのか実験してみました。総レシピ数を25と16にした場合の結果は以下の通りです。
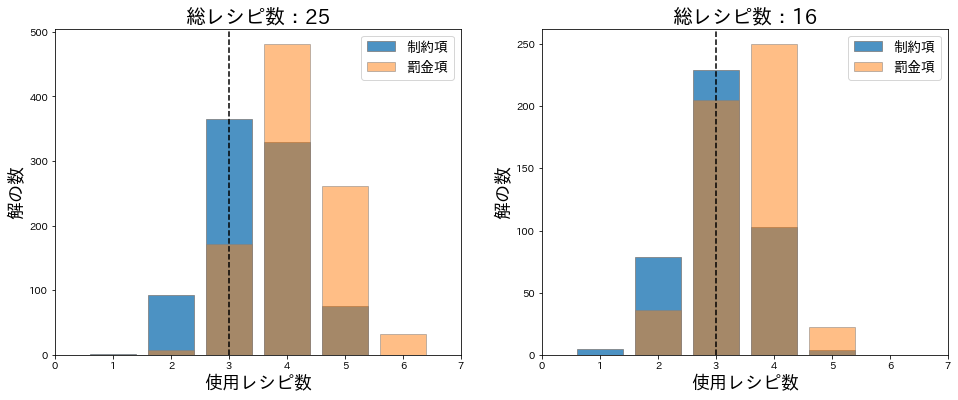
ここまで減らせば献立として使える解(使用レシピ数が2と3)が出てきました。しかし、総レシピ数が少なすぎてアプリケーションとしては非実用的ですね。
そこで、ハイブリッドソルバーの出番になります。アルゴリズムは非公開となっていますが、大規模な組み合わせ最適化問題も条件を満たしつつ解けます。ただ、ハイブリッドソルバーの利用は高価なので、ダミーデータで使うのは避けた方が良いです。次章では実際のレシピデータで実験した結果をご紹介します。
5. D-Waveハイブリッドソルバーの性能評価
この章は弊社が開発/運営するボブとアンジーのレシピデータを用いた検証結果になります。妥当な献立提案を実現するために諸々の条件を課したものになっています。
5.1. 処理時間
まず、ハイブリッドソルバーの処理時間についてです。
QA自体は1回20マイクロ秒で終わるので、サンプリング数1,000でも20ミリ秒で終わります。しかし、問題サイズが大きい(今回だと総レシピ数が多い)と現在の量子アニーリングマシンには問題が乗り切りません。これは古典コンピュータで物理メモリが足りない状況と似ています。そこで、問題を分割したり古典的な手法で計算したり、QA以外の計算で補う必要が出てきます。ハイブリッドソルバーのアルゴリズムは公開されてませんが、QA自体は一瞬で終わるため計算時間のほとんどが古典的な計算と考えられます。
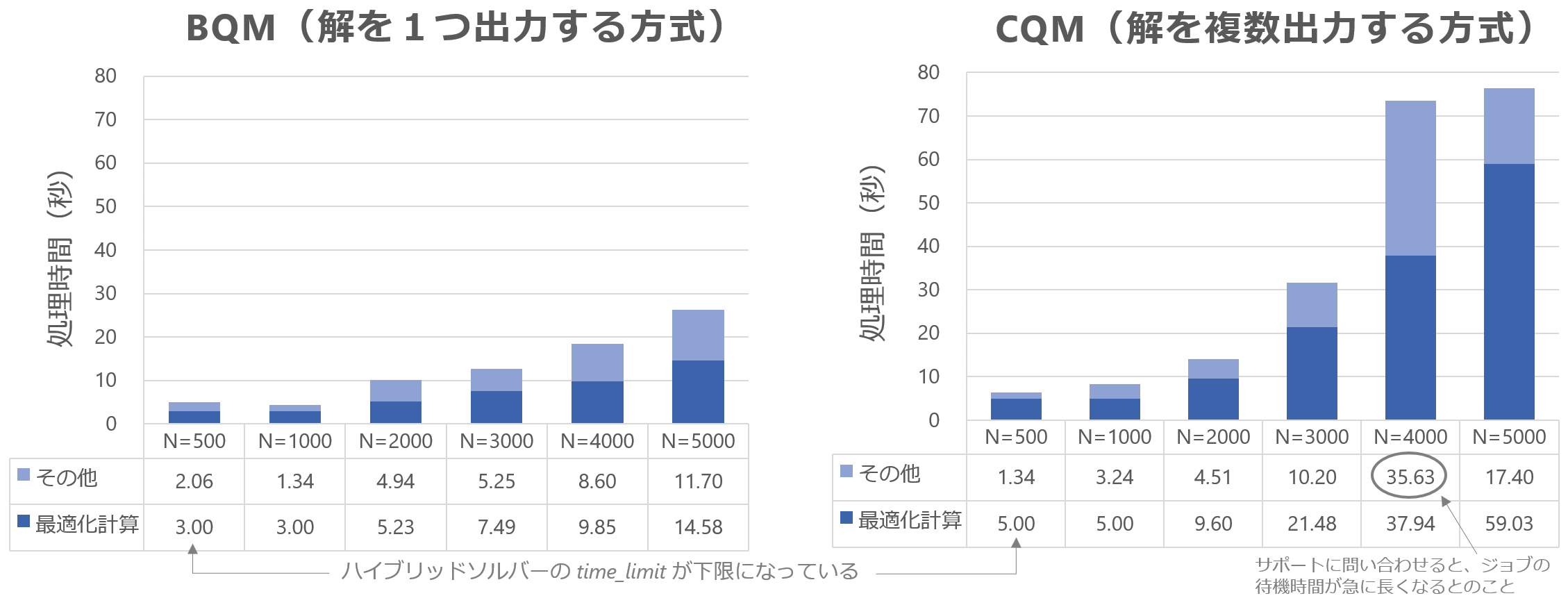
次のグラフはハイブリッドソルバーを問題サイズ(下図では N と表記)を変えながら実行した結果です。
濃い青で表示された最適化計算の時間はAPIかD-Wave Leapのコンソールで確認できます。APIだと実行結果 response から response.info で取得できます。執筆時点で公式ドキュメントの出力例は
{'qpu_access_time': 41990, 'charge_time': 2991424, 'run_time': 2991424}
でした。単位はマイクロ秒です。
上図で最適化計算の時間には run_time の値を使っています。charge_time はオーバーヘッドを除いた値で、課金対象となる利用時間に対応しています。qpu_access_time は純粋なQAの実行時間ですが、総計算時間に比べて非常に短いです(上の例だと計3秒のうち42ミリ秒だけ)。
図に戻って最適化計算の時間を見てみると、N = 500 と N = 1,000 の計算時間は下限にぶつかっています。そのあとはBQMは線形で増加、CQMは指数関数的に増加しています。解の出力方式が異なるので、計算方法も異なると思われます。
その他に含まれる主な時間にデータの転送時間があります。データの転送時間は実機との物理的な距離が近いほど短くなるので、実機に近いAWSのオレゴンリージョンに立てたEC2インスタンスから実行しています。素直に日本から実行すると、BQMの N = 4,000 でその他の時間が 32 ~ 36 秒掛かりました。日本からの実行時間はオレゴンと比べて4倍近く掛かっています。ハイブリッドソルバーに限らずD-Wave社のマシンを利用する際は実機との物理的な距離にご注意ください。
また、CQMの N = 4,000 でその他の時間が急に増えています。何度実行しても同じ結果なので、D-Wave社に問い合わせたところ、N = 4,000 のあたりでジョブの待ち時間が急に長くなる仕様になっていたとのこと3。開発チームに問い合わせてもらって何通かやり取りしてようやく回答を得たので、原因が分かるまで2か月も掛かりました。量子技術開発は今がまさに黎明期で、こういった事情は実際に使ってみないと分からないところです。逆に開発側からすると使ってもらって初めて認識することもあると思うので、ユーザとしては使ってみて分かったことを発信することが重要だと考えています。
5.2. 手法ごとの性能比較
次に、ハイブリッドソルバーの性能を古典的な手法であるSAとシミュレーテッド量子アニーリング(SQA)と比較してみます。上の実装ではSAのサンプリング数は1,000で動かしてましたが、ここではSAとSQAのサンプリング数は50に減らしてます。そのくらいでないとハイブリッドソルバーと比較にならないくらい時間が掛かるためです。
結果は以下のようになりました4。
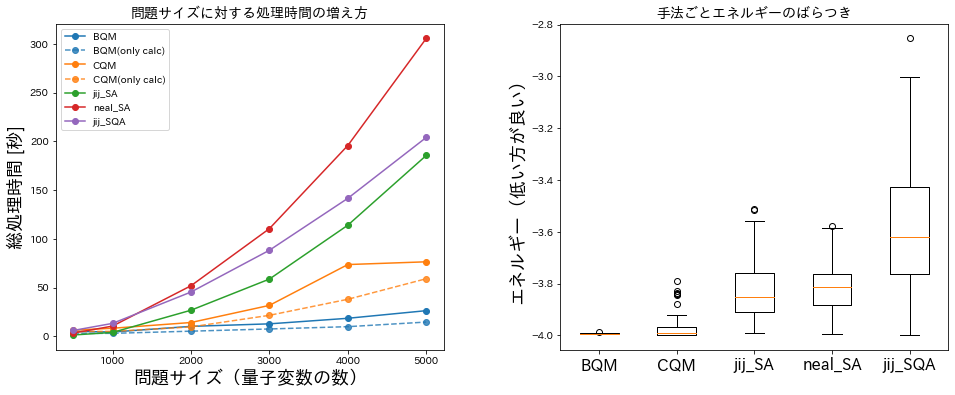
参考のため、株式会社Jijさんが開発しているOSS(openjij)も利用しています。前出のD-Wave社のSAより高速なことが特徴です。
左の図で青がBQM、オレンジがCQMの処理時間です。点線は最適化計算だけの時間です。問題サイズが大きくなるとハイブリッドソルバーの方がSAやSQAより2倍以上速いですね。計算時間のほとんどが古典的な計算と述べましたが、高速化のために色々な工夫がなされていると思います。
右の図は N = 3,937(デモ用に抽出したレシピの総数)における最適化の精度を表したものになります。BQMは最良解を1つだけ返す仕様のため複数回実行した結果を示しています。CQMは1回の実行で複数の解を返す仕様で、この時は53個の解が得られています。CQMに少し外れ値がありますが、ハイブリッドソルバーはどちらも精度の良い解が得られています。
SAとSQAも最良解はハイブリッドソルバーと同程度のものが得られています。ただし、精度の良い解が得られるかどうかは運任せ(乱数次第)になります。安定して良い解が欲しい場合はサンプリング数を1,000とか10,000に増やせば良いのですが、計算時間とのトレードオフになります。
また、前回記事で具体的に提案された献立を比較した際にも述べましたが、SAは局所解に陥りやすく最良解であっても一部の項目だけ目標から大きく離れていることが多いです。ハイブリッドソルバーは全項目がバランスよく目標に到達している点も強みです。
結論としては、ハイブリッドソルバーはSAで動かしてたものをそのまま高速化+高精度化できるという点でメリットがあると言えます。デメリットは費用が掛かるという点ですが、どのくらい掛かるのかはD-Wave社にお問い合わせ頂ければと思います。
6. さいごに
想定より長い記事になってしまいましたが、前回と合わせて2021年度の取り組みを紹介させていただきました。
次回は2022年度の取り組みとしてゲート方式の量子コンピュータを使った話を考えています。具体的には、弊社が参画している量子ソフトウェア研究拠点で開催された2022年度量子ソフトウェア勉強会のグループワーク成果になります。
なお、その内容は 5/10(水)-5/12(金) 開催の量子コンピューティングEXPOに出展します。量子ソフトウェア研究拠点のブースにてポスター展示を行います。さらに、ブース内でのモニターを使ったプレゼンも実施予定です。ご都合のつく方はぜひ足を運んでいただければと思います。
-
今回実装しているQUBO行列は対象行列になっていて、(i, j) 成分と (j, i) 成分は同じ値です。情報圧縮のため (i, j) 成分が2倍され、(j, i) 成分が 0 になった上三角行列に置き換えることもできます。コストは両成分の和で与えられるので、置き換え前後でコストは変わりません。 ↩
-
"最適解"と書くと語弊がありそうなので、サンプリングで得られた中で一番良かった解という意味で"最良解"と書いています。 ↩
-
問い合わせ時点(2021年12月)での話なので既に改善されている可能性があります。 ↩
-
SAとSQAはAWS EC2の
t3.xlargeインスタンスで実行しています。ちなみにt3.large(メモリ8GB)だと N = 5,000 でメモリ不足になったので、t3.xlarge(メモリ16GB)にしています。 ↩