過去2回は量子アニーリングを用いた記事でしたが、今回からゲート方式の量子コンピュータを扱います。次回から実際に量子コンピュータの実機を使いますが、今回はその前に理論をざっとおさらいするという位置づけです。量子コンピュータについて学ぶ教材も増えてきたので、オリジナリティあるまとめ方にしました。
目次
1. はじめに
量子コンピュータは従来のコンピュータ(古典コンピュータ)を扱うことに比べると、とっつきにくい印象がある方が多いかもしれません。その理由は2つあると考えていて、それぞれに対して本記事ではどういうスタンスで臨むのか表明しておきます。
- 量子力学という理論が背景にあるため数式や専門用語が多くハードルが高い
新しいことを学ぶというのは自分にとって既知の物事とのギャップを埋めることと言えます。ただ、そのギャップがあまりにも大きいと、理解できない、もしくは理解をあきらめるという結果になりがちです。
そこで、本記事では古典コンピュータの計算が論理回路からなることと対応して、量子コンピュータにおける論理回路(ゲート演算)を起点に話を進めます。
教科書より平易に、それでいて体系的に一直線に理解できることを心掛けました。実用性を意識した構成で、量子力学の教科書とは違う論調になっているかと思います。
- そもそも物質の量子的な振る舞いが我々が普段体験することとかけ離れておりイメージしにくい
これは物理学の研究者であっても同様です。アインシュタインも量子の不思議な性質が直感と反しているとして否定していました。しかし、実験により古典的には説明できない事実が次々と明らかになります。量子力学はその中からこれ以上原理原則に追究出来ない経験的な事実を土台に構築されました。その際に、理論に課した要請を公理と呼びます。
これでうまくいったとはいえ、これでは公理に不思議なことを押し付けただけです。それでも理論にとって公理はそれ自体を納得する必要はなく受け入れるしかありません。ある意味あきらめでも構いません。実際そうでもしないと前に進めなかったのが量子力学だったのです1。
量子コンピュータの理論を学ぶにあたって、疑ってはいけない暗黙の了解である公理を念頭に置かないと、理解できないことがあっても自分がどこでつまずいているのか分からなくなります。
とはいえ、公理を並べてから始めても困惑すると思うので、本記事では一連のストーリーの中で必要になったタイミングで量子力学の公理を紹介することにします。
また、本連載では量子コンピュータを使うことが目的なので数式の導出が天下りになることがあります。一方で、物理的な意味合いは丁寧に説明したつもりです。『入門』と銘打ったのは、教科書と違って数式ではなく感覚として理解できればとの思いです。難しいことを避けたというわけではなく、今後エキスパートになるための土台となることを目指しました。発展的な内容やコラム的な内容は注釈にしています。すでに専門知識がある方にも読んでなるほどと思っていただければ幸甚です。
2. 演算の理論
まず量子コンピュータの演算方法について解説します。
古典コンピュータが論理回路で計算されるように、量子コンピュータは量子コンピュータにおける論理回路(量子回路)で計算されます。本章ではその量子回路を構成する論理ゲートの演算(ゲート演算)がどのような操作になっているか説明します。
2.1. ユニバーサルゲートセット
古典コンピュータは NAND 論理ゲートさえあれば任意の論理回路を作ることができ、どんな演算も可能です。これを万能性といいます。
ここで NAND 論理ゲートは2つのビット値を入力し1つのビット値を出力する演算で、次のような変換を行います。
- 古典 NAND 論理ゲート
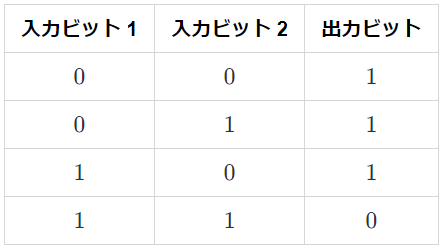
AND, OR, NOT のような一般的な操作も NAND 論理ゲートで表現できます。たとえば、ビット値を反転させる NOT 論理ゲートは2つの入力に同一のビット値を入れると実現できます。上表で入力ビット 1 と入力ビット 2 が共に 0 であれば出力ビットは 1 に、1 であれば 0 になっていますね。
ゲート方式の量子コンピュータもその名の通りゲート操作によって演算を行います。古典コンピュータにおける論理回路と論理ゲートが量子コンピュータでは量子回路と量子論理ゲートになります。
量子コンピュータの場合は H(アダマール)ゲート、T ゲート、CNOT(制御 NOT)ゲートという3種類の量子論理ゲートがあれば万能性があることが知られています。それらはまとめてユニバーサル(万能)ゲートセットと呼ばれていて、それぞれ以下のような操作です。
- H(アダマール)ゲート:重ね合わせ

- T ゲート:位相シフト

- CNOT(制御 NOT)ゲート:量子もつれ

急に新しい記法や専門用語がバンバン出てきました。本章ではこれらの意味が理解できるよう順に説明します。
2.2. 1量子ビットの状態
まず量子ゲートの入出力表に書かれた |0〉と |1〉は古典コンピュータにおけるデジタル(離散的)なビット値 0, 1 ではなく量子状態というものを表しています。読むときも単なる数値と区別して |0〉は 0 Ket(ケット)と読みます。Ket というのは造語で、括弧を表す bracket から閉じ括弧を意図して右側の Ket だけ取り出したものです。開き括弧に対応する 〈0| は 0 Bra(ブラ)と読みます。Bra については次章で登場します。
古典ビットは 0 か 1 ですが、量子ビットは |0〉かつ |1〉が可能です。この |0〉と |1〉が共存する性質は重ね合わせと呼ばれますが、経験的なものでなぜそれが可能なのかは説明できません。つまりこれは量子力学における公理のひとつです。
この公理を受け入れると、1量子ビット状態 |ψ〉は数式で
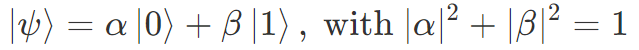
と書けます。|0〉と |1〉の係数 α, β は複素数であることに注意してください。α と β の絶対値2乗の和が 1 になることも公理から要請しています(この公理については次章で説明します)。
上式で重要なのは量子ビットは離散的な値ではなく連続的な値を取るアナログなものということです。古典ビットと違い、量子ビットの |0〉と |1〉は連続的に繋がっています。
数式だとよく分からないかもしれませんが、ブロッホ球と呼ばれる可視化手法を用いると幾何学的にイメージができるようになります。 |0〉と |1〉をブロッホ球で表示すると以下のようになります2。
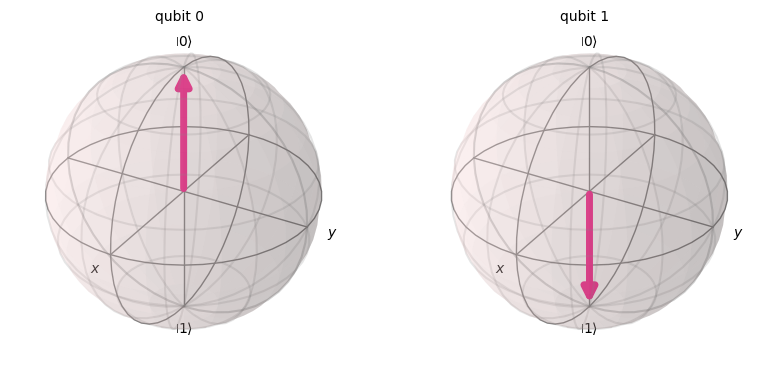
ブロッホ球では |0〉と |1〉は Z 軸上の点で表され、図では原点からその点に向かう矢印で示されています。座標値で言うと、|0〉は (x, y, z) = (0, 0, +1)、|1〉は (x, y, z) = (0, 0, -1) です。
ほかの量子状態もブロッホ球の球面上の点として表現されます。量子状態を変化させるということはその点を球面に沿って移動させることと等価です。
2.3. パウリゲート
以下、量子状態を変化させる操作(ゲート操作)をブロッホ球面上の点を移動させる操作として説明します。
まずイメージしやすいものとして、ブロッホ球における各軸周りでの 180 度(ラジアン表記で π)回転操作を考えます。これはパウリゲートと呼ばれる操作で、以下のような出力になります。
- X ゲート:X 軸周りの π 回転

- Y ゲート:Y 軸周りの π 回転
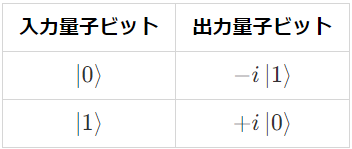
- Z ゲート:Z 軸周りの π 回転

X ゲートは単純に |0〉と |1〉を入れ替える操作ですが、Y ゲートでは虚数 i が登場しています。虚数 i に限らず、量子状態に現れる大きさ 1 の複素数(α を任意の角度として eiα で表される数)は位相(位相因子)といいます。Z ゲートの操作は |1〉の位相を +1 から -1 に変換しているので位相反転とも呼ばれます。
これらのパウリゲートは2回連続で操作すると元の状態に戻るという性質があります。各ゲートが 180 度回転操作なので、2回操作つまり 360 度回転すると元に戻ります。これは赤道上で地球を 360 度ぐるっと一周回ったら元の場所に戻るのと同じ理屈です。
2.4. 行列表現
ここでゲート操作を表す記法として行列表現を導入します。
入力量子ビットを
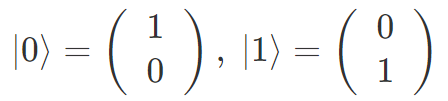
とおくと、パウリゲートは以下のように書けます。
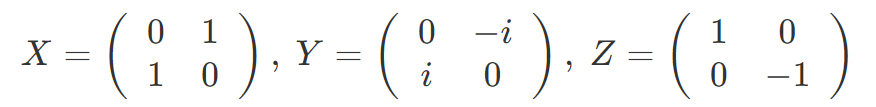
出力量子ビットは各行列を入力量子ビットに掛けることで得られます。たとえば、X ゲートの操作は
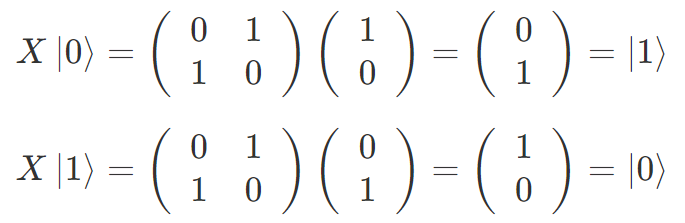
となります。前節で示したように入力の |0〉と |1〉を入れ替える操作になっていることがわかるかと思います。
行列表現を使うとゲートを続けて操作した結果が簡単に計算できます。たとえば、X ゲートと Z ゲートの順操作は
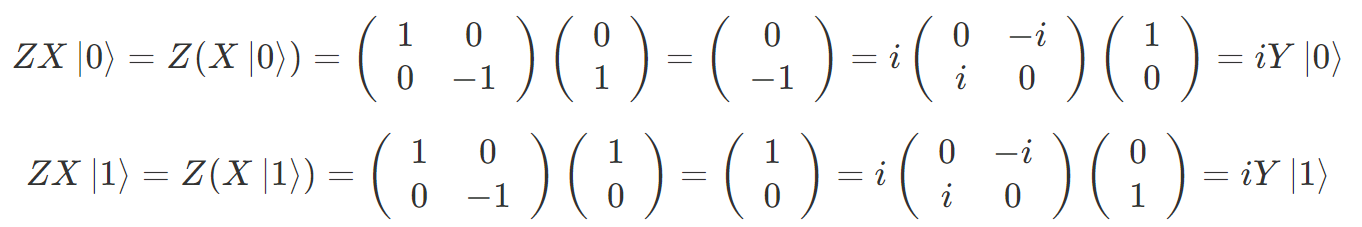
となり、Y ゲートの操作に位相 i が掛かった状態になります。全体に掛かる位相は物理的には不要なものとして無視できる3ため、X ゲートと Z ゲートの順操作は Y ゲートの操作と等価と言えます。
他のパウリゲート同士の順操作も同様です。パウリゲートがこのような循環性を持つことは覚えておいてください。
2.5. 回転ゲート
パウリゲートは 180 度回転でしたが、任意の角度 Θ だけ回転させることも考えられます。任意の回転ゲートがあれば量子状態をブロッホ球面上の任意の点に移動させることができます。導出は省きますが、それらは以下のような操作になります。
- RX ゲート:X 軸周りの Θ 回転
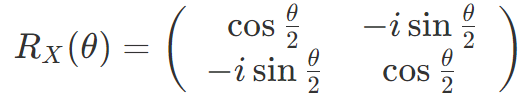
- RY ゲート:Y 軸周りの Θ 回転
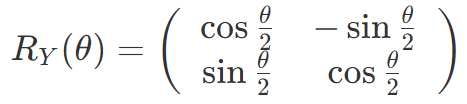
- RZ ゲート:Z 軸周りの Θ 回転
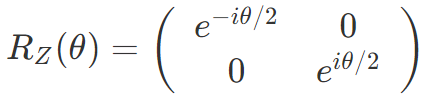
各操作で Θ = π とすれば、全体に掛かる位相を除いて先ほどのパウリゲートと一致します。
最初に紹介したユニバーサルゲートセットのひとつである T ゲートは Θ = π / 4 の RZ ゲートと等価です。T ゲートを4回続けて操作すれば Θ = π の RZ ゲート、つまり、Z ゲートになります。先ほど Z ゲートの操作を位相反転とも呼びましたが、T ゲートのように反転までいかない回転操作は位相シフトと呼ばれます。
また、興味深いのは RX ゲートと RY ゲートで4つの要素がすべて 0 でない場合です。たとえば、Θ = π / 2 のときは以下のようになります。
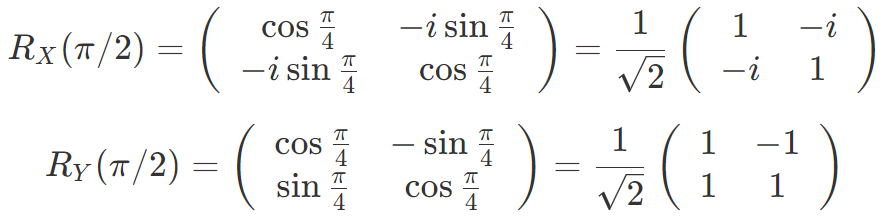
これを入力量子ビットに操作するとどうなるでしょうか。RY ゲートの方だけ書くと
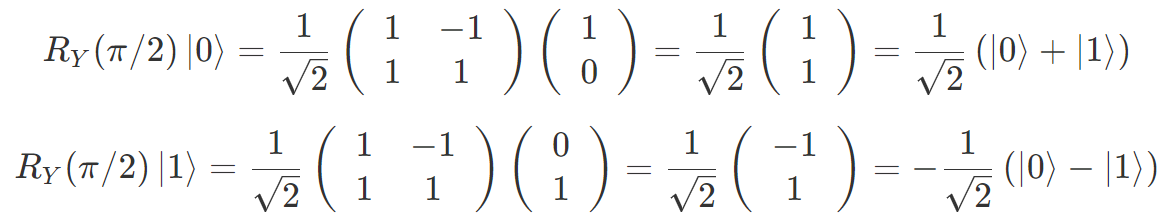
これは Y 軸周りに Θ = π / 2(90 度)回転した状態なので、ブロッホ球でいうと X 軸上の点になっています4。ブロッホ球で見ると以下のようになっています。
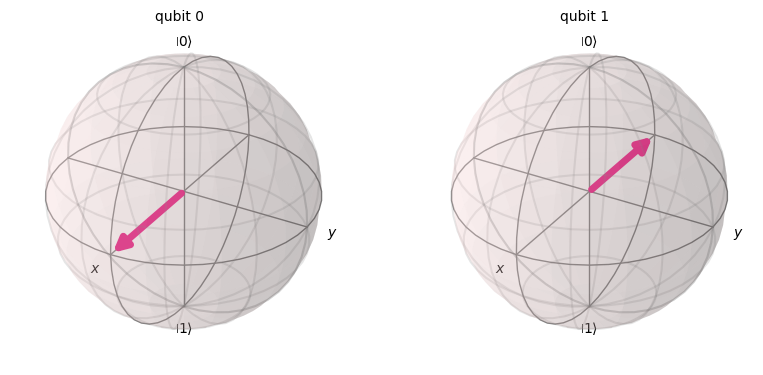
左が |0〉+ |1〉で、右が |0〉- |1〉です(係数は省略)。この |0〉でも |1〉でもなく両方が混在した状態は重ね合わせ状態といいます。重ね合わせ状態の特性については次章で測定について説明する際に言及します。
X 軸上にある量子状態は以下のように略記されることが多いです。
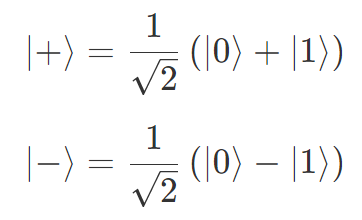
以降、この略記も使いますのでご留意ください。
2.6. H(アダマール)ゲート
次に、ユニバーサルゲートセットのひとつである H ゲートを説明します。H ゲートは行列で書くと
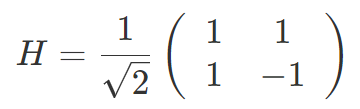
で、操作後は以下のようになります。
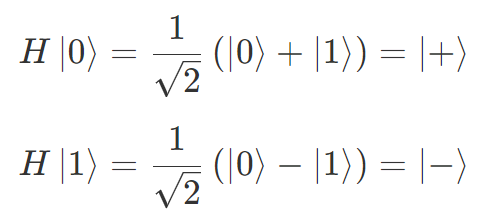
このように H ゲートは重ね合わせ状態を作る操作となっています。
先ほどの RY ゲートと比べると入力 |1〉に対して出力量子ビットの符号が逆になっているだけの違いですが、この H ゲートを前節の回転ゲートで表現するのは少し複雑です5。
幾何学的には H ゲートはブロッホ球の X 軸と Z 軸を入れ替える操作に対応しています。上のブロッホ球の図では右手系(X 軸、Y 軸、Z 軸の正の方向をそれぞれ “右手” の親指、人差し指、中指でさせる系)で定義されており、H ゲートはそれを左手系(X 軸、Y 軸、Z 軸の正の方向をそれぞれ “左手” の親指、人差し指、中指でさせる系)に変える操作です。
この軸の入れ替え操作を使うと以下の等式が成り立ちます。
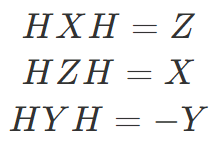
つまり、X 軸と Z 軸を入れ替えてから X ゲートを操作して再度 X 軸と Z 軸を入れ替えると、元の系で Z ゲートを操作したことと等価になります。逆もまたしかりです。Y ゲートを操作した時だけ符号が反転した Y ゲートになります(左手系に移った系を右手系と捉えると Y 軸が反転するため)。これらの等式はパウリゲートの行列表現を使えば簡単に示せるので導出は省略します。
また、単なる軸の入れ替えと考えれば当然ですが、H ゲートを2回連続で操作すると元に戻ります。
2.7. I(恒等)ゲート
ここで、何もしない操作を恒等ゲート
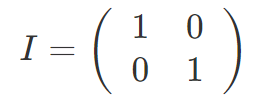
として定義すると
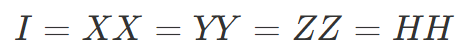
が成り立っています。パウリゲートと H ゲートは2回操作すると何もしてないのと同じという意味です。
当たり前ですが、回転ゲートも Θ 回転したあと - Θ 回転すれば元に戻ります。
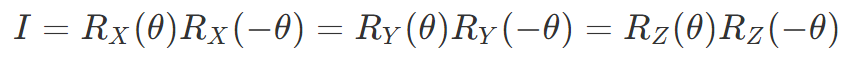
これらの等式も各ゲートの行列表現から容易に示せます。
2.8. 1量子ビット演算のユニバーサルゲートセット
ところで、H ゲートも T ゲートとならびユニバーサルゲートセットのひとつでした。1量子ビットに対する操作はこれで網羅できるので確認してみます。
まず Z ゲートは T ゲート4回と等価でした。
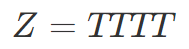
また X ゲートは Z ゲートと H ゲートを使って表せました。
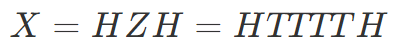
残る Y ゲートはパウリゲートの循環性から X ゲートと Z ゲートの順操作と等価でした。
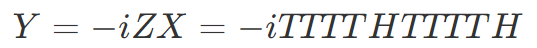
あとは任意の回転操作ですが、T ゲートは Z 軸周りの π / 4 回転で、これを基準とするとそれ以上こまかい回転操作はできなさそうに思えます。しかし、直感的には理解しがたいかもしれませんが、任意の回転が有限回のゲート操作で精度良く近似できることが知られています6。
一例として、Z 軸周りの -π / 8 回転を 10-4 精度のゲート操作で表すと以下のようになります7。精度というのは、この右辺のゲート群を行列で表すと 2.5 節で紹介した理論上の RZ ゲートとの差が 10-4 程度になるという意味です。
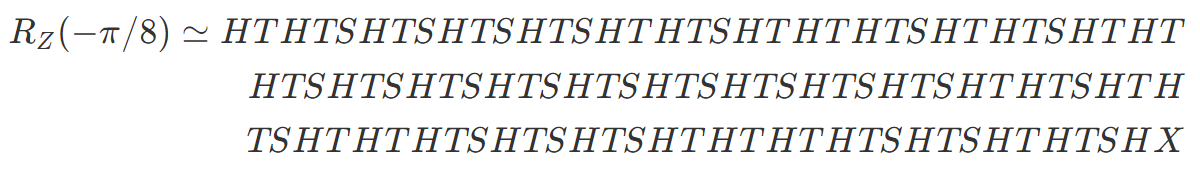
ここで、右辺に現れている S ゲートは Z 軸周りの π / 2 回転操作、つまり T ゲート2回で
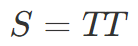
です。右辺の最後にある X ゲートも H ゲートと T ゲートで表せたので、Z 軸周りの -π / 8 回転はユニバーサルゲートセット(H ゲートと T ゲート)の操作だけで表せました。ほかの回転角度も同様にユニバーサルゲートセットの操作だけで表せます。
ところで、T ゲート2つをわざわざ S ゲートと名付けているのには理由があります。T ゲートがないと万能性はないのですが、量子回路が S ゲートと H ゲート(と後述の CNOT ゲート)だけで構成されるなら古典コンピュータで効率良くシミュレートできます8。逆に言うと、古典コンピュータを超えるには T ゲートの存在が重要です9。
2.9. 複数量子ビットの状態
ここまで1量子ビットだけでしたが、ここからは複数量子ビットについての話です。
まず複数量子ビットの状態を書く記法を説明します。
1量子ビット状態の一般式は |0〉と |1〉を基底に取り、それらの線形和で表せました。2量子ビット状態の基底は1つ目の量子ビットと2つ目の量子ビットの状態を左から順に並べるだけで
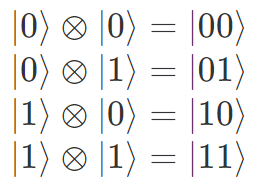
と書きます(⊗ はテンソル積)。右辺は単なる省略表記ですが、上から順に 0, 1, 2, 3 の2進数表記になっていることが特徴です。
3量子ビット状態は 0 から 7 まで2進数表記で並べたものになります。量子ビットがさらに増えても同様で、N 量子ビットであれば2進数表記で 0 から 2N - 1 まで、計 2N 個の基底があります。
N 量子ビットの量子状態 |ψ〉をそれら基底の線形和で表すと
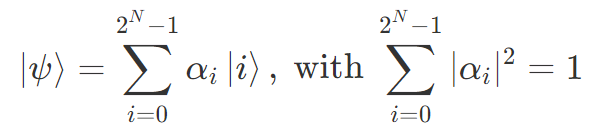
と書けます。右辺の量子状態 |i〉は i を2進数表記したものに対応します。
量子状態 |i〉のベクトル表記は、2N 個の要素を持ち、上から i 番目の要素だけ 1 で他が 0 のベクトルです。たとえば、N = 2 で i = 3(2進数で 11)の量子状態は
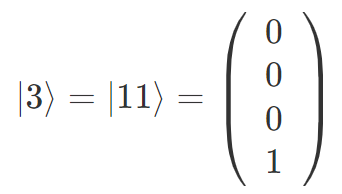
で表されます。i は 0 から数え、i = 3(上から 4 つ目)だけ 1 になっていることに注意してください。以降でも、量子ビットは 0 番目、1 番目、… と数えていくことにします。
このような複数量子ビット状態に1量子ビットゲートを操作するときは、明示的に何番目の量子ビットに対するゲートか添え字を付けておくことにします。
たとえば、以下のように書きます。
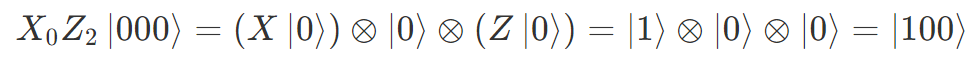
2.10. CNOT(制御 NOT)ゲート
2量子ビットゲートで重要なのは CNOT ゲートです。ユニバーサルゲートセットの残りのひとつで、複数量子ビットの操作はこれだけあれば万能です。
CNOT ゲートは行列で書くと
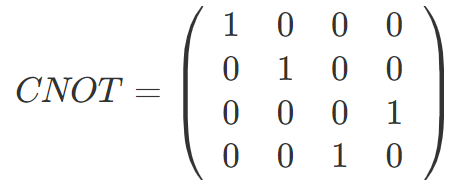
となっていて、2量子ビットの状態に対して |10〉と |11〉を入れ替える操作になっています。
この操作は 0 番目の量子ビットが |1〉の時だけ 1 番目の量子ビットを反転させています。そのため、起点となっている 0 番目の量子ビットをコントロール(制御)量子ビット、反転対象となる 1 番目の量子ビットをターゲット(対象)量子ビットと呼びます。
複数の量子ビットがある場合、制御量子ビットと対象量子ビットに指定する量子ビットは任意なので、それぞれ何番目の量子ビットか明示的に示す場合は CNOTi,j と書くことにします。i 番目の量子ビットが制御量子ビット、j 番目の量子ビットが対象量子ビットです。
そのほかの2量子ビットゲートや3量子ビットゲートは CNOT ゲートと1量子ビットゲートに分解できます。具体例は次回以降に紹介します。
2.11. もつれ状態
CNOT ゲート単体ではとくにおもしろいことはありませんが、H ゲートと組み合わせると量子の不思議な性質が現れます。
まず |00〉という初期状態に対して 0 番目の量子ビットに H ゲートを操作すると
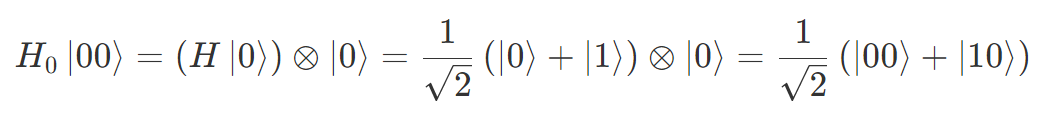
になります。この状態に CNOT ゲートを操作すると |10〉が |11〉になるので
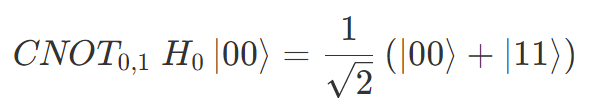
という状態になります。片方の量子ビットが |0〉ならもう片方の量子ビットも |0〉、|1〉なら |1〉という状態です。これはベル状態として知られています。
このベル状態では2つの量子ビットが独立していません。言い換えれば、ベル状態は 0 番目の量子状態 ⊗ 1 番目の量子状態 の形(1つの項だけ)で書けません。CNOT ゲート操作前の状態は 0 番目の量子ビットが重ね合わせ状態ですが |+〉⊗ |0〉という1つの項だけで書けます。
ベル状態のように複数の量子ビットの状態を分けて記述することができない状態はもつれている(エンタングルしている)といいます。同様にもつれ状態(エンタングル状態)という使われ方もします。この現象のことは量子もつれ(エンタングルメント)と呼ばれます。
ベル状態に代表されるもつれ状態の性質は次章で測定について説明した後に再考します。
3. 測定(観測)の理論
この章で説明するのは量子状態の測定(観測)についてです。
測定は前章のゲート操作とはまったく異なる操作です。量子力学の直感と反する現象の多くが測定に絡んでいて非常に難解な概念となっています。ここからはほぼ公理と言っても過言ではなく、説明はできないけどそういうものだという論調になりがちです。
本記事ではなるべくイメージができるようにブロッホ球を用いた表現で説明しています。類書に見られない表現で、言葉による説明が多いので逆に難解になっているかもしれません。より分かりやすい説明を目指した挑戦的な試みということでご了承いただければと思います。
3.1. 測定方法の任意性
これまで1量子ビット状態として
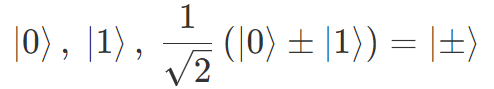
が出てきましたが、これら量子状態を測定する方法は一意ではなく、測定方法によって結果が変わります。
これは量子状態がブロッホ球面上の点で描かれることを思い出すとイメージしやすいです。というのも測定というのはブロッホ球におけるどの軸から値を読むのかということに対応しています。
慣例的に測定はデフォルトでは Z 軸の値を読むこととなっています。
|0〉と |1〉のブロッホ球表示はそれぞれ以下のようになっていました。

|0〉は (x, y, z) = (0, 0, +1) の点に対応するので Z 軸の値を読む測定(Z 測定)をすると +1 が得られます。同様に、|1〉は (x, y, z) = (0, 0, -1) に対応するので Z 測定すると -1 が得られます。測定後の値 v は v → (1 - v) / 2 という置き換えをすれば、|0〉は +1 → 0、|1〉は -1 → 1 となり、古典的なビット値に対応させることができます。
次に、重ね合わせ状態 |±〉について考えてみます。この状態は Z 軸上にある |0〉と |1〉を Y 軸周りに 90 度回転することで実現できました。ブロッホ球でイメージすると、下図のように Z 軸上の点が X 軸上の点に移ることが分かります。

そのため、重ね合わせ状態 |±〉は X 軸の値を読む測定(X 測定)をすると |+〉は +1、|-〉は -1 が得られます。上の例と同じように 0 と 1 のビット値に置き換えることもできます。
一方で、|±〉はブロッホ球面上で z = 0 の点なので、Z 測定するといずれも 0 になります(?)。0 は置き換えると 1 / 2 になってしまい、ビット値ではありません。量子ビットの値も測定すると 0 or 1 のように2値になることが知られているのですが、なんだかおかしいですね。
実はここまでの議論で大きな飛躍をしていました。誤りを訂正しながら測定という操作の詳細を追っていきます。
3.2. ボルンの確率規則
まず以下の文を訂正します。
|±〉はブロッホ球面上で z = 0 の点なので、Z 測定するといずれも 0 になります(?)。
|±〉がブロッホ球上で z = 0 だから Z 測定値も 0 というのは誤った推論でした。実際には、重ね合わせ状態を Z 測定しても +1 か -1 のどちらかしか得られません。|±〉が z = +1 の |0〉と z = -1 の |1〉が重ね合わされた状態だったということを思い出してください。測定ではそのどちらかの状態が確率的に選ばれることになります。
ただし、このどちらかしか選ばれないという選択則は説明できない経験的事実でボルンの確率規則と呼ばれる公理です。この公理ではなぜ測定値が確率的に振る舞うのかは説明しませんが、ある測定値が得られる確率は教えてくれます。
はじめに一般の量子状態は
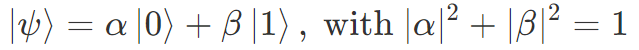
と書けると紹介しましたが、この量子状態を1回だけ Z 測定すると |α|2 の確率で +1、|β|2 の確率で -1 が得られるというのがボルンの確率規則です。
α と β は絶対値2乗が確率になるので、それらは確率振幅と呼ばれます。実は、確率の和が足して 1 になるという要請から |α|2 + |β|2 = 1 という規格化条件が課されていました。
3.3. 射影仮説
ボルンの確率規則によって
重ね合わせ状態を Z 測定しても +1 か -1 のどちらかしか得られません。
ということでしたが、実験から Z 測定後の量子状態は |0〉か |1〉に変わっていることが分かっています。これも説明できない経験的事実です。そこで量子力学では射影仮説と呼ばれる公理を導入しています。
射影仮説は Z 測定するとブロッホ球の Z 軸上にある |0〉か |1〉の状態に収縮することを要請します。収縮するというのは専門用語で、即時に遷移するという意味です。量子状態は Z 測定値が +1 なら |0〉に、-1 なら |1〉に収縮します。
同様に、射影仮説は X 測定の場合はブロッホ球の X 軸上の状態にある |+〉か |-〉に収縮することを要請します。量子状態は X 測定値が +1 なら |+〉に、-1 なら |-〉に収縮します。
このように測定値は ±1 で変わりませんが、測定した方向に沿った状態になるという性質があります。そのためここでいう測定は射影測定とも呼ばれます。他の測定手法もありますが、本記事では扱いません。
また、物理的に重要なのは測定の「即時性」と「不可逆性」です。
即時性は、測定後の遷移がまさに即時的であるため X 測定と Z 測定を同時に行うような同時測定が禁止されているということです。たとえば、|+〉を Z 測定すると |0〉か |1〉になりますが、X 測定すると必ず |+〉のままです。この両者は相いれず、同時測定という操作自体が不可能であるためと説明されます。
不可逆性は、測定後の収縮した状態が自然に元の量子状態に戻ることはないということです。古典的なゲート操作は入力が2ビットで出力が1ビットになる不可逆な操作ですが、量子コンピュータのゲート操作はすべて入出力の量子ビット数が同じ可逆な操作で、この測定という行為のみ不可逆な操作です10。
3.4. 測定=期待値計算
次の見直しポイントは以下の文です。
というのも測定というのはブロッホ球におけるどの軸から値を読むのかということに対応しています。
ここでは1回だけ軸の値を読むという感じですが、測定という用語は同じ量子状態を用意し軸の値を読むということを何度も繰り返し、読み取った値の平均を取るという意味で使われることがほとんどです。
ボルンの確率規則により、重ね合わせ状態 |±〉は Z 測定すると確率 1/2(50%)で |0〉か |1〉のどちらかの状態になることが分かります。この測定を何度も繰り返す(試行回数を増やす)と平均値は 0 に近づいていきます。現実的には有限回の測定しかできないので平均値がちょうど 0 になることは稀で、ここでいう 0 は期待値(原理上期待される値)です。
|±〉はブロッホ球面上で z = 0 の点なので、Z 測定するといずれも 0 になります(?)。
実はこの表現は1回の測定では間違いでしたが、期待値という意味では正しい表現になっていました。
ところで、1回ごとの測定値である ±1 は v → (1 - v) / 2 という置き換えをすれば古典的なビット値である 0 と 1 に置き換えることができましたが、測定の期待値には古典コンピュータでの対応物がありません。古典コンピュータで同じ計算を何度させても毎回同じ答えが返ってくるからです。あえて言えば、古典コンピュータでの期待値=1回の計算結果でしょうか。いずれにせよ古典コンピュータにとって同じ計算は1回だけで十分なのに対し、量子コンピュータは何度も同じ計算をさせないといけないというのは大きな違いです11。
3.5. 期待値の計算方法
ここでボルンの確率規則を用いて期待値の計算式を求めてみます。
一般の量子状態に対して
この量子状態を1回 Z 測定すると |α|2 の確率で +1、|β|2 の確率で -1 が得られるというのがボルンの確率規則です。
だったので、Z 測定の期待値(確率 × 値 の総和)は
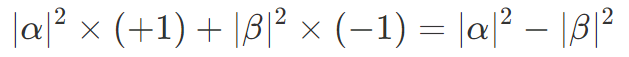
になります。
次に、X 測定する場合を考えます。
X 測定はブロッホ球における X 軸の値を読み取る操作ですが、これは量子状態を X 軸上の状態である |±〉を基底として式変形することに対応しています。実際に式変形すると、基底の変換は以下のようになります。
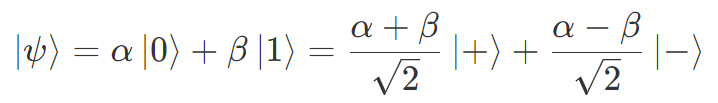
この |±〉の係数がブロッホ球における X 軸の値で、X 測定における確率振幅です。よって、X 測定の期待値は
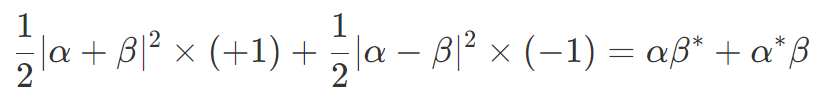
になります。ここで * は複素共役のことで、複素数 α、β の虚部(虚数 i の係数)を符号反転させています。
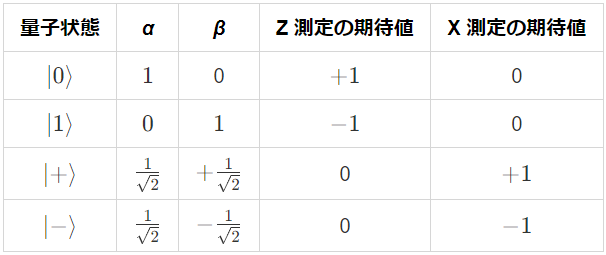
このように同じ量子状態でも測定方法によって期待値は異なります。主な量子状態に対する期待値は以下にまとめておきます。
3.6. 行列表現による期待値計算
前節の期待値を求める計算式ですが、前章のゲート操作で用いた行列表現を使うと簡単に導出できます。
まず一般の量子状態はベクトル表記で
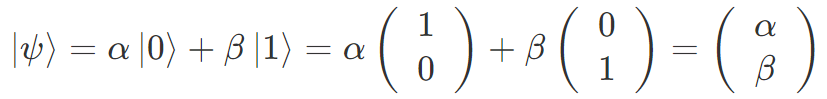
と書けます。これのエルミート共役(複素共役と転置)を取ったものを
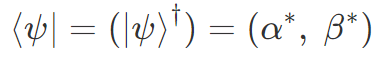
と定義します(† がエルミート共役を表しています)。2.2 節で頭出ししましたが、これまで扱ってきた Ket(ケット)状態に対して、この逆向きの記号は Bra(ブラ)状態を表しています。
Bra と Ket という言葉は括弧(bracket)のように挟んで使うことに由来しています。
各測定の期待値はパウリゲートを Bra と Ket で挟んであげると計算できます。
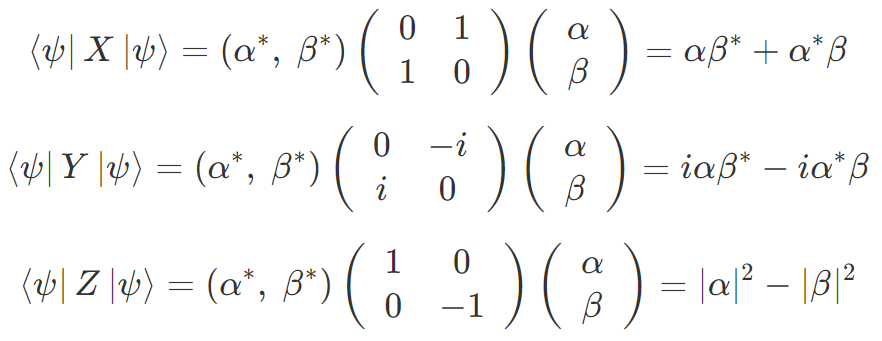
X 測定と Z 測定の期待値は前節での結果に一致しています。Y 測定の期待値は計算していませんでしたが、行列表現を使えば簡単に求めることができました。
3.7. 物理量(可換測量)の条件
測定についてもうひとつ重要なことがあります。
測定できる量のことを物理量(可換測量)と言いますが、測定値である物理量が実数でなければならないという要請があります。
私たちが現実に住む世界には数値が溢れていますが、それらはすべて実数です。虚数は数学上登場することはあっても何かを測定したら虚数だったということはありません(我々が虚数計測器を持たず、虚数をそのまま認識できないだけという可能性もありますが)。
前節で求めた各測定の期待値は複素数である確率振幅で表されています。それらがすべて実数になっているか確認してみましょう。
Z 測定の期待値は確率振幅が絶対値2乗でのみ登場しているので実数です。X 測定と Y 測定の期待値については一般的な複素数の性質から
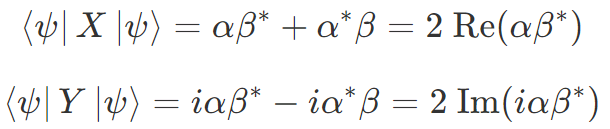
と計算できます。ここで Re(・)、Im(・) はそれぞれ括弧内の複素数から実部、虚部の値のみ取るという操作で、いずれも実数を返します。そのため、X 測定と Y 測定の期待値も実数です。
逆に、期待値に虚数が現れない条件を考えると、期待値計算の真ん中に入れたゲートがエルミートでなければいけないことが要請されます。エルミートというのはエルミート共役(複素共役と転置)を取ったものが自身と等しいという性質です。パウリゲートは行列表現を見て明らかなように、すべてエルミートです。
物理量が実数でなければならないことの裏返しとして、このエルミート性に関する記述が量子力学では公理になっています。
しかし、ゲート操作の行列がエルミートであれば測定できるわけではありません。H ゲートはエルミートですが
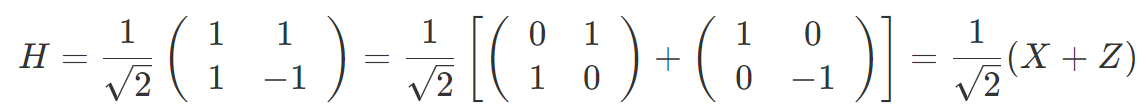
のように X ゲートと Z ゲートに分解されます。もし H 測定できるとすれば、X 測定と Z 測定の和が得られます。しかし、3.3 節で述べたように、射影仮説は X 測定と Z 測定の同時実行を禁止しているので、H 測定と呼ばれるものはありません。
そのほか回転ゲートは Θ = 2 n π(n は整数)以外の角度だとエルミートではありません。
試しに RY ゲートの期待値を計算してみると
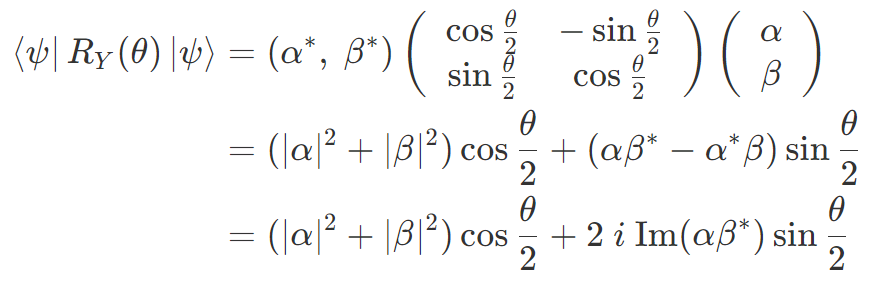
となり、2項目が虚数です。この2項目が 0 になる角度以外では期待値が実数にならないので測定できません。
虚部が 0 になる Θ = 2 n π(n は整数)だけが許されますが、それは恒等ゲート I に対応します。その期待値は
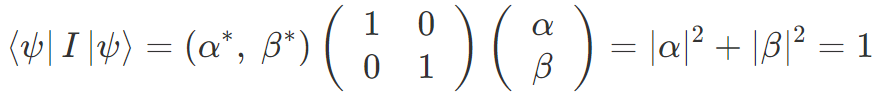
です。どんな状態を I 測定しても期待値は 1 になります。
ということで、許される測定方法は限られており、量子ビットの物理量としては X、Y、Z、I 測定の期待値だけが登場します。
3.8. もつれ状態の測定
本章の最後に、もつれ状態の測定について考察します。
2.11 節で紹介したベル状態は2つの量子ビットが共に |0〉か共に |1〉という状態で、以下のように書かれました。
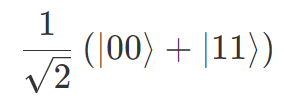
結果から言うと、この状態を測定すると次のようになります。
- 0 番目の量子ビットを Z 測定すると同確率(確率 50%)で +1 か -1 が得られる(ボルンの確率規則)
- Z 測定値が +1 なら 0 番目の量子ビットの量子状態は |0〉に収縮、-1 なら |1〉に収縮(射影仮説)
- このとき同時に 1 番目の量子ビットも 0 番目の量子ビットと同じ状態に収縮している
- つづけて 1 番目の量子ビットも Z 測定すれば確率 100% で 0 番目の量子ビットと同じ測定値が得られる
この結果ははじめに測定する量子ビットを 1 番目の量子ビットに変えても同様です。
太字で示した3ステップ目がもつれ状態と呼ばれる所以で、1つの量子ビットの測定が2つの量子ビットの状態を同時に確定しています。これは古典的な観点だと非常に不思議な現象です。物理的に距離が離れていて互いに情報のやり取りをしなくても、片方の測定結果が即時にもう片方の状態に影響を与えているのです。
もし重ね合わせ状態ではなく |00〉か |11〉のどちらかが古典的な手法で確率 50% ずつで用意できるとすればどうなるでしょうか。ただ Z 測定するだけであれば、ベル状態と同じ測定結果が得られると考えられます。
しかし、すぐに測定するのではなく、測定前にゲート操作があると重ね合わせ状態とそうでない状態に違いが生じ得ます。
たとえば、CNOT0,1 と H0 を順に操作すると、単一の状態であれば
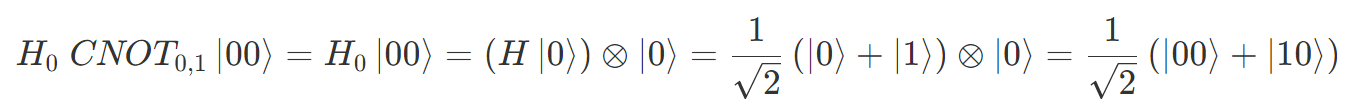
もしくは
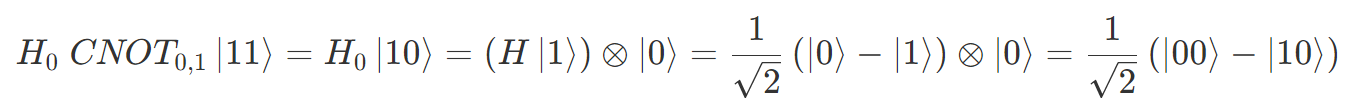
になりますが、ベル状態だと
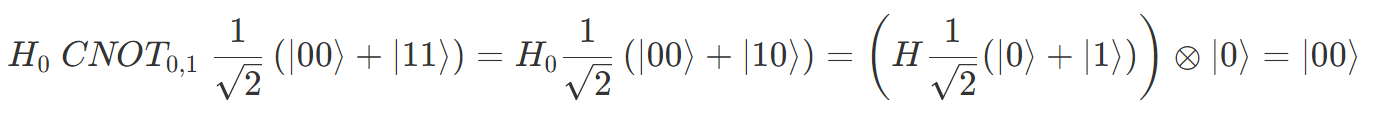
になります。0 番目の量子ビットを Z 測定すると、単一の状態の方は確率 50% で +1 か -1 が得られますが、ベル状態だった方は確率 100% で +1 が得られます。つまり、「古典的な確率に基づいて複数の状態を用意すること」と「量子的な重ね合わせ状態」は同一視できません12。
ベル状態のように量子もつれと重ね合わせが同時に現れる状態が量子計算の真髄です。測定するまですべての可能性が捨てられず、全可能性が干渉し合って未来の計算結果も変えうる。SF チックな響きですが、それが現実で、それを理解して活用しようというのが量子コンピュータになります。
4. 量子力学の公理
本章では量子力学の公理をまとめます。
公理というのは、これ以上原理原則に追究出来ない経験的な事実を導くために理論に課す要請のことです。
ここまでに登場した公理は以下の4つです。
| 公理 | 概説 | 登場箇所 |
|---|---|---|
| 重ね合わせ状態 | 量子状態は取りうる状態の線形和で表される | 2.2 節 |
| ボルンの確率規則 | 1回の測定でどの状態が得られるかは確率で決まる | 3.2 節 |
| 射影仮説 | 測定すると瞬時に1つの状態に定まる | 3.3 節 |
| 物理量の条件 | 物理量は実数(行列のエルミート性) | 3.7 節 |
量子力学にはあともうひとつ、量子状態の時間発展はシュレーディンガー方程式に従うという公理があります。シュレーディンガー方程式は
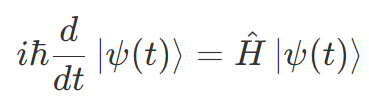
で表されます。この式で横棒つきの h はプランク定数というただの数で、Ĥ はハミルトニアンと呼ばれるものです。ハミルトニアンは系のエネルギーを表すものですが、以下ではそれがエルミートであることのみ意識します。
ハミルトニアンが時間依存しない場合、この方程式は以下のように解くことができます。
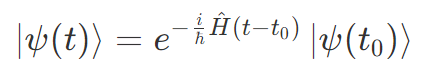
右辺の |ψ(t0)〉はある時刻 t0 における量子状態のことです。これに e・ を掛けると時刻 t における量子状態 |ψ(t)〉になるという式です。
ここで e・ の部分はハミルトニアンがエルミートなのでユニタリーになります。行列 U がユニタリーであるとき
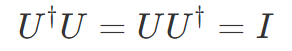
を満たします。ここで † はエルミート共役(転置と複素共役)を取るという意味です。
上の量子状態の時間発展はユニタリー行列を用いて
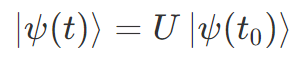
と一般化できます。
ゲート操作も量子状態の時間発展なので、ゲート操作の行列表現はユニタリーでなければいけません。2章では色々なゲートを天下り的に紹介しましたが、すべてユニタリーであることが容易に確かめられます。また、ゲート操作がユニタリーであったからこそ、量子状態がブロッホ球の球面上の点であり続けます。
シュレーディンガー方程式は量子力学のはじめに出てくることが多いですが、量子コンピュータの文脈だと出てこないこともあります。量子コンピュータに不要なわけではなく、暗黙のうちにゲートのユニタリー性に落とし込まれています。
最後に、量子コンピュータの観点で公理をまとめて終わりにします。

5. さいごに
なかなか長い記事になってしまいました。これでも量子コンピュータの実機に紐づけられる内容は削ったのですが。次回は実際に量子コンピュータを使うので、実機に関連した押さえておくべき知識はそこで紹介できればと思います。
今回記事を書くにあたってこれまでに私が学んだ知識をフル動員したので、多数の文献を参考にさせていただいています。読書案内として3冊だけ紹介して本記事を閉じたいと思います。
- 『量子コンピュータ入門[第2版]』(日本評論社)宮野健次郎、古澤明 著
- 大学初年度レベルを対象とした入門書。量子コンピュータを一躍有名にした素因数分解を行うショアのアルゴリズムや実際に計算するのに必須な量子エラー訂正など実用的な内容を分かりやすい説明でコンパクトに学べる。
- 『量子コンピューティング 基本アルゴリズムから量子機械学習まで』(オーム社)情報処理学会出版委員会 監修、嶋田義皓 著
- 量子コンピュータに関連した事柄が網羅的にまとめられていて非常に参考になる一冊。話題が豊富だが、内容によっては高難度。手元に置いて辞書的に使うのが便利。
- 『新版 量子論の基礎』(サイエンス社)清水明 著
- 量子力学から学ぶならオススメしたい教科書。副題が「その本質のやさしい理解のために」となっており、本質の理解に主眼を置いている。ただし、物理や数学に慣れ親しんだ人でなければ“やさしい"とは感じない可能性あり。
-
これはコペンハーゲン解釈と呼ばれる主流派のことで、量子力学の公理に納得せず新たな理論を構築する研究分野もあります。ご興味を持たれた方には様々な理論を網羅的にまとめた書籍として『量子力学の諸解釈』がおすすめです。 ↩
-
1量子ビット状態の全体に掛かる位相は3章で説明する測定では打ち消されて出てきません(測定では絶対値の2乗が意味を持つため)。ただし、続けて2量子ビットのゲート操作を行う場合は全体の位相も意味があるので、計算の途中で省いてはいけません。 ↩
-
同様に、X 軸周りに π / 2 回転した状態はブロッホ球の Y 軸上の点になっています。この状態については次回の記事で扱います。 ↩
-
H ゲートに限らず(ユニタリー行列で表現される)任意の量子ゲートは RX ゲートと RZ ゲートに分解できます。こちらの講義資料が参考になりました。H ゲートの回転行列による分解の例は 18 ページに載っています。 ↩
-
これは Solovay–Kitaev の定理と呼ばれています。藤井先生のセミナー資料の 12 ページから続く説明が視覚的に分かりやすいので、納得いかないと感じた方はぜひご一読ください。 ↩
-
論文 "A Software Methodology for Compiling Quantum Programs” (arXiv:1604.01401) から抜粋。論文には 10-10 精度のゲート操作も載っています。 ↩
-
S ゲートと H ゲート、CNOT ゲートはクリフォードゲートと呼ばれ、クリフォード群の要素になっています。クリフォードゲートとパウリゲートの関係を使うと測定で得られる結果を効率良く計算できます(Gottesman-Knill の定理)。 ↩
-
しかし、T ゲートは実現コストがほかのゲートに比べて格段に大きいと考えられています。T ゲートが量子コンピュータと古典コンピュータを隔てるものと言えますが、今のところそのギャップは大きいです。ほかにも今の量子コンピュータには制約が多く、どのようなゲートを使うべきかは量子回路の最適化という問題で精力的に研究されています。 ↩
-
測定の即時性と不可逆性を情報理論的に考えてみます。2つの入力が1つの出力になる不可逆な操作では状態数(選択肢の数)が減り、意味のある情報は増えます(不確実さが減るという意味で)。古典的な演算ではゲート操作のたびに意味のある情報に変換されていくのに対し、量子コンピュータにおけるゲート操作はその時点で意味のある情報にはならず、測定という特殊な操作を施した瞬間に意味が生まれることになります。つまり、量子コンピュータは測定する最後の瞬間まで何も分かりません。もしゲート操作による演算の途中で今どんな感じかなと測定してしまうと、量子状態が変化してしまいその後の計算結果が変わってしまいます。量子コンピュータによる計算では途中でログ出力して経過を確認するようなことはできないのです。この性質は不便に感じるかもしれませんが、盗聴される(盗聴には必ず測定操作が含まれる)とその事実が明らかなので、暗号技術への応用が期待されている根拠にもなっています。 ↩
-
ときおり量子コンピュータは古典コンピュータに比べて圧倒的に速いという言説が流れますがその中身には注意が必要です。量子コンピュータにおける1回の測定に掛かる時間はマイクロ秒(1 秒の 100 万分の 1)の単位ですが、測定を何回も実行して平均値を得ることでようやく意味を持ちます。その平均値が小数点以下6桁の精度で必要ということであれば、少なくとも 100 万回の測定が必要なので、1つの値を得るのに秒スケールの時間が掛かることになります。また、量子回路のパラメータを変えながら 100 回繰り返したり、1つでなく 100 個の値を求めたいとなれば、さらにその倍で 100 秒スケールになります。このように量子コンピュータによる計算時間は求める数値の精度と求める数値の数の掛け算でスケールします。実際に量子化学計算で意味のある値を求めようとすると膨大な時間が掛かってしまうという研究結果もあります(参考文献)。一方で、1回の測定で意味を持つようなアルゴリズムを考えるアプローチもあります。その場合は古典計算に対する優位性があるのかが重要です(未調査の領域なのでこれ以上の言及は避けます)。 ↩
-
物理的には前者は混合状態、後者は純粋状態として区別されます。量子状態を密度行列と呼ばれる記法で表せば両者の違いを表現できます。本記事では本編のストーリーにうまく乗らなかったので必要であれば次回以降に説明します。 ↩
