暗号モジュールのテストはなぜ難しいか

暗号ライブラリなどのような暗号機能を提供するモジュールのテストには特有の困難さが潜んでいることを、皆さんはご存知でしょうか？実は入力の全組み合わせテストは非常に困難です。困難な理由とテスト手法を解説します。

はじめに

本稿では、暗号モジュール（共通鍵暗号、公開鍵暗号、ハッシュ関数などの暗号機能を提供するもののこと。ソフトウェアやハードウェア、あるいはその組み合わせなどにより実現する）のテストについて解説します。

暗号ソフトウェアを移植した際などに「暗号化→復号して元に戻ったから大丈夫！」という動作確認をしている方がしばしばいらっしゃるのですが、残念ながらこの方法では不十分です。この方法では正しい暗号文になったことが確認できていません。A+1-1=Aになっても、A+1が正しく計算できているとは限らない、と言えばイメージしやすいでしょうか？間違いがあって弱い暗号文が生成されていると暗号を解読されてしまう危険があります。

では、正しい暗号文はどうやって用意すれば良いでしょうか？また、テストはどのくらいの組み合わせを行えば良いでしょうか？

実は暗号モジュールの入出力テストを「完全に」行うのは非常に困難です。本稿では困難な理由を解説し、対処方法を紹介します。

目次：暗号モジュールのテスト

• 全組み合わせテストのデータサイズは？
• 暗号の性質
• テストベクタ
• おわりに

全組み合わせテストのデータサイズは？

まず、暗号モジュールの入出力テストを「完全に」行うのが困難、ということについて説明します。

AES-128の暗号モジュールを例にとります。入力は平文（暗号化される前の生のデータ）と鍵、出力は暗号文です。平文も鍵も暗号文も128bitなので、それぞれ16Byteずつですね。

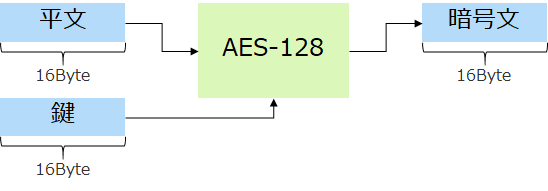
16Byteというと小さく聞こえるでしょうか？しかし、bitが128個あるということは取り得る値の組み合わせは2x2x2x…と128回繰り返した数、つまり2¹²⁸（≒3.4x10³⁸）通りという莫大な数になります。128bitでは桁が大きすぎて内容を説明しにくくなるので、まずは8bitの暗号モジュールを仮定して考えてみたいと思います。

8bit暗号のテストデータ

8bitの平文の場合、1Byteの値が256通り存在します。0x00（00000000b）～0xFF（11111111b）ですね。鍵も1Byteとすると平文と鍵で256 x 256 = 65536通りの組み合わせがあります。

テストデータを作るなら入力に対応する出力（正解データ）も用意する必要がありますので、暗号文1Byteも同じ数だけ必要です。試験仕様書兼試験成績書のイメージを作ってみました。（暗号文の値は適当です。ランダムっぽい値になっていますね。この辺の性質については次の章で触れます）

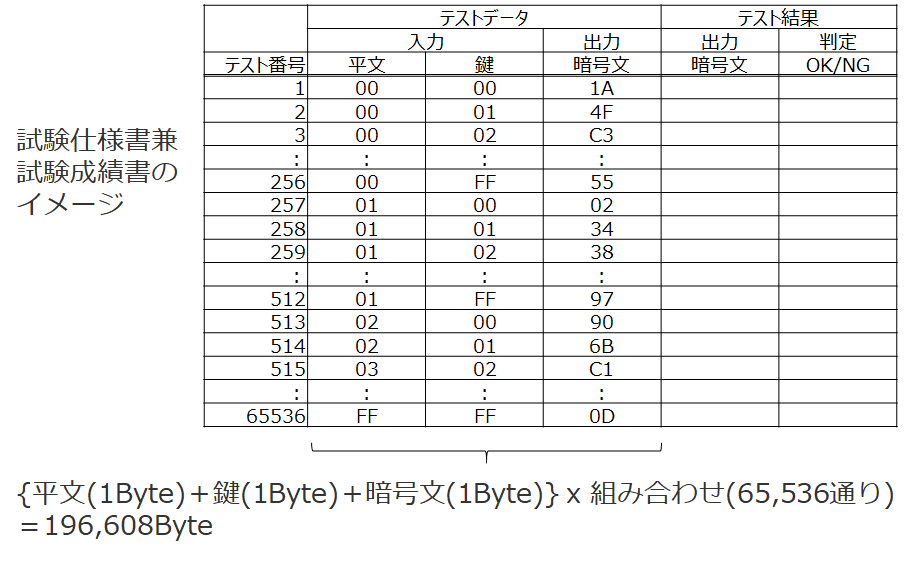
テストデータの大きさは196,680Byte（192kByte）ということになります。ただ、これはフォーマットも何も考えず、バイナリデータを順番決め打ちで詰め込んだ場合の値です。扱いやすいようにASCII文字にして区切り文字や改行コードなどを加えた場合、サイズは数倍に膨れ上がるでしょう。とはいえ1MByte前後には収まりそうです。

128bit暗号のテストデータ

では、同じように128bit（16Byte）のテストデータの大きさを計算してみましょう。

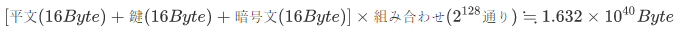
約1.6x10⁴⁰ Byteです。40桁ですね。日本で日常に使われる単位はせいぜい兆（10¹²。国家予算なんかで聞きますね）までですから、10⁴⁰は巨大すぎてイメージが湧かないかもしれません。試しに、テストデータをHDDに格納するつもりで考えてみたいと思います。

2020年現在普及しているHDDのうち容量の大きなものは10TB(1,099,511,627,776Byte)くらいです。これを10億(1,000,000,000)台用意します。置き場所だけでも大変なことになりそうですが、国や巨大IT企業が本気になれば何とかなるかもしれません。この合計容量は、

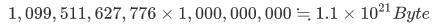
約1.1.x10²¹Byteです。うーん残念、19桁も乖離しているので兆までの単位では説明できません。

仕方ないので適当に少し未来を仮定して水増ししましょう。なあに、1980年代にはHDDは10MB (10TBのおおよそ100万分の1)くらいだったのです。HDDのサイズはさらに100万倍になることにしましょう。10PB(1,152,921,504,606,846,976Byte)です。HDDの台数も1,000倍に増やせることにしましょう。どーんと1兆(1,000,000,000,000)台です。用意できたストレージは、

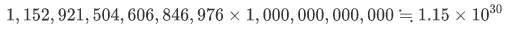
約1.15x10³⁰Byteです。

未来を先取りして10PBのHDDを1兆台用意しても、テストデータ容量(1.6x10⁴⁰)にざっと10桁（100億）足りない、つまりテストデータ全体の100億分の1も入らないことが分かりました。

フォーマットでさらに数倍に膨れ上がる話に触れるまでもなく、これではとても全組み合わせテストに必要なテストデータを用意することはできないと言えます。

暗号の性質

しかし、なぜこんな問題が起きるのでしょうか？これには暗号特有の性質が関係しています。

大抵のプログラムは入力に任意のデータ列を受け取れるとしても、完全な全組み合わせテストまでは行いません。境界値、異常値などの有意な条件や、代表値、ランダム値などの運用でありそうな条件に絞ってテストを行います。テストを効率的に行うために、他のテストと同じような結果になると考えられる条件は省略するのが普通です。

ぴんと来ない方のために、単純な処理を例に説明します。説明が不要な方は読み飛ばして「暗号の場合」へ進んでも大丈夫です。

単純な処理の場合

仮に「8bitのデータに対し、1bit左シフトする」プログラムを作ったとしましょう。8bitの全組み合わせ(00000000～11111111までの256通り)に対してテストが必要でしょうか？

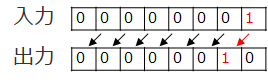
まず、各bitがそれぞれ個別にシフトされるかを確認するテストをbit0～7まで全部やることにしましょう。8通りですね。

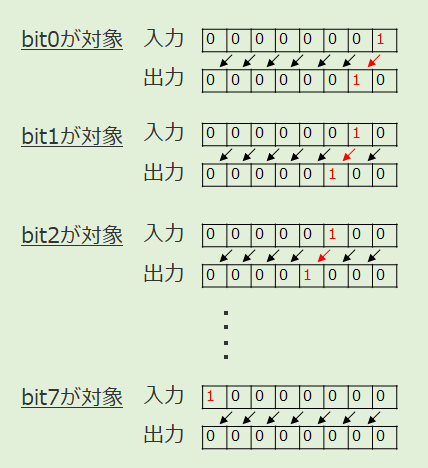
次に、同時に2つのbitが立っても互いに干渉しないことを確認するテストについて考えてみます。8つのbitから2つを選ぶため、₈C₂=28通りです。こちらは、幾つか（bit0と1が対象～bit0と7が対象までの7通り）だけやっておけば、他の組み合わせは省略できるかもしれません。他の場合でも各bitの持つ性質や振る舞いは同じになると推測できるからです。

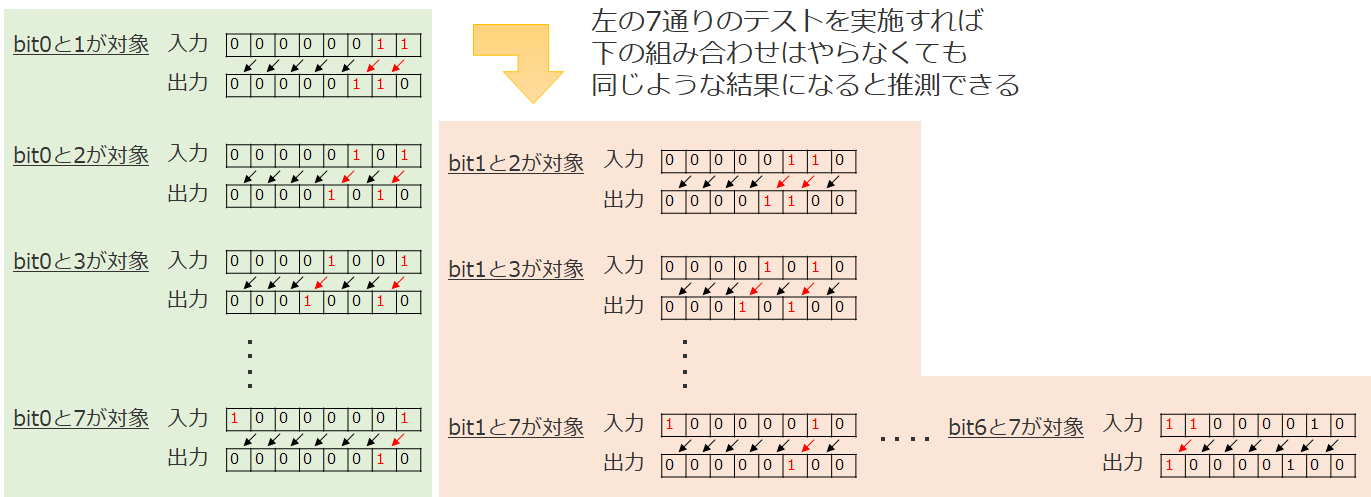
ブラックボックステストという観点で見ればこれはもちろん「推測」に過ぎませんから、この7通り以外の組み合わせも何通りかやっておくべきかもしれません。念のため28通り全てをやるという考え方だってあるでしょう。しかし、さらにその後同じように3つのbitが立つ場合（₈C₃=56通り）や、4つのbitが立つ場合（₈C₄=70通り）についてはどうでしょうか？実施済みのテストから結果が推測できる組み合わせを省略するのは、合理的な考え方と言えます。

暗号の場合

ところが、暗号においては事情が違います。

暗号には「他のテストと同じような結果になると考えられる条件」を見つけるのが難しいという性質があります。暗号とは「入力（平文）と出力（暗号文）に推測可能な依存関係がない（乱数のように出力が予測できない）」ものだからです。平文と暗号文に分かりやすい依存関係があったら簡単に解読できてしまいますからね。

8bit暗号モジュールの動作イメージを図にしてみました。

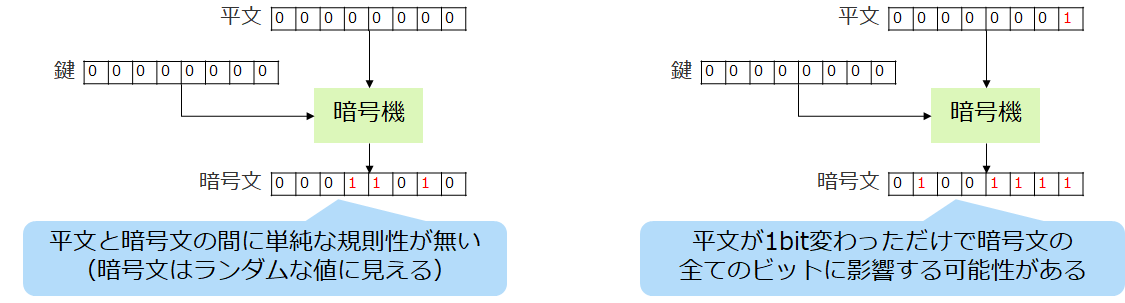
平文が1bitでも変われば暗号文の全bitのどれが変わるか分かりません。1bitかもしれないし全bitかもしれません。また、同じbitが変わるかもしれないし違うbitが変わるかもしれません。（さらに、実は平文を固定して鍵を1bitだけ変えても、暗号文の全bitが変わる可能性があります）

そのためどの組み合わせを省略するのが妥当か、判断するのはなかなか難しいという訳です。

前の章でテストデータを用意するのが難しいという説明をしましたが、実は現代の主要な暗号アルゴリズムの多くは、完全なテストデータを用意することが困難である（あるいは用意できたとしても試すのに非現実的な時間がかかる）ことを主要な安全性の根拠の1つとしています。

完全なテストデータがあれば、たった1組の平文と暗号文のペアを手に入れるだけで暗号解読ができてしまいます。データを検索すればその平文と暗号文のペアに対応する鍵の値はすぐに特定されてしまいますから、その鍵から作られるすべての暗号文を解読できる（対応する平文が分かる）ことになるのです。

言い換えると、そもそも全組み合わせテストは現実的に不可能なように設計されているわけです。

テストベクタ

それでは暗号モジュールのテストはどのように行えばよいのでしょうか？

CAVP（Cryptographic Algorithm Validation Program。米NISTのSTVMグループが公開している暗号アルゴリズムの検証制度プロジェクト）で提供されているような、信頼できるテストベクタ（Test vector。テストに必要なデータ一式のこと）を通すのが一般的なやり方です。

アルゴリズムの性質やコンピュータアーキテクチャの性質から、問題が起きそうな（バグがあったら見つけられそうな）データ列（桁上り処理が発生するとか、データ長を見て条件分岐する場合とか）を考えて用意してくれています。

ここまでは暗号を例に説明してきましたが、メジャーな暗号の多くは数式が出てきてややこしいので、比較的分かりやすい処理が出てくるハッシュ関数SHA-1を例に具体的に説明します。

SHA-1の例

ハッシュ関数は可変長の入力メッセージを固定長のデータ列に変換する処理です。入力はメッセージだけ、というシンプルなインターフェイスを持ちます。

さて、SHA-1の中にはパディング（入力メッセージを処理しやすい長さに整える）処理があります。この仕様はRFC3174 (4.Message Padding)によると以下のように書かれています。

（略）The message or data file should be considered to be a bit string. The length of the message is the number of bits in the message (the empty message has length 0).（略）The purpose of message padding is to make the total length of a padded message a multiple of 512. SHA-1 sequentially processes blocks of 512 bits when computing the message digest.（略）As a summary, a “1” followed by m “0"s followed by a 64-bit integer are appended to the end of the message to produce a padded message of length 512 * n. The 64-bit integer is the length of the original message.

簡単に日本語で要約するとこんな感じです。

• SHA-1の入力はbit stringとして受け取る。
• 長さはbit単位で扱い、入力メッセージ無しは長さ0とする。
• 処理を512bitブロック単位で行うから、長いメッセージは分割する。
• 分割した最後のブロックは512bitになるようにパディングする。
• パディング規則は以下。
  • メッセージの直後に1を付ける
  • 1の後ろは（下記「長さ」の64bitも含めて）512bit単位になるように0で埋める
  • 末尾に元メッセージの長さ値を64bitの整数で格納する

パディング後の最終ブロックのデータは次の図のような構造になります。

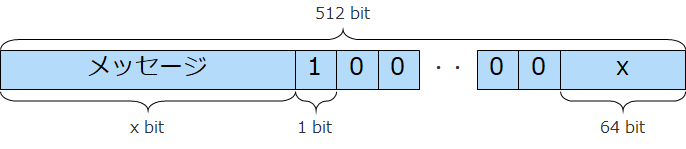
入力メッセージの長さに関して、仕様から気になる（テストが必要そうな）のは以下のような場合でしょうか。

• 長さ0の境界
  • メッセージの長さ＝0bitの場合
  • メッセージの長さ＝1bitの場合
• パディング後が512bitに収まる場合と越える場合の境界¹
  • メッセージの長さ＝446bitの場合
  • メッセージの長さ＝447bitの場合
  • メッセージの長さ＝448bitの場合

もちろんCAVPのテストベクタはこれらの場合を網羅しています。

以下にCAVPのテストベクタを抜粋します。Lenが入力メッセージの長さ、Msgが入力メッセージ、MDが出力ハッシュ値です。

Len = 0 Msg = 00 MD = da39a3ee5e6b4b0d3255bfef95601890afd80709

Len = 1 Msg = 00 MD = bb6b3e18f0115b57925241676f5b1ae88747b08a

Len = 446 Msg = f00191c9d258d6584fa1fa351b53e1c7d327b4a3838783a56b432f40038787123c0ab1bc0987ccf01e71d3ccf7e3c4661dd602a8a596f85c MD = db1acdd6da00f434b270838ef98bade4cc8371d0

Len = 447 Msg = de11fa659cc16ad64de598bf7403be07b14d1b7de62f3b0f98247a3c98cdc4cce2449ebec5ae6a82440fe668bd63f759c8eaa5c562c366dc MD = 14c764e1369c26aa6a92e75384ea6394986d706b

Len = 448 Msg = 06024501b3a1b703e79089f132ad71b99a7d3322971ec25e627da8e26fc9a9753827a3873da7b9c54976b0eaf65699d8734cb1e78598857d MD = 8d405e3332002c4b645721fa38a78c2f99796e17

ちなみに、実はCAVPには上記5通りだけでなく、長さ0bitから512bitまでの513通りが全て用意されています。

上記ではパディングのアルゴリズムに着目してテストを検討しましたが、コンピュータアーキテクチャやプログラミング言語の仕様から、他の様々な長さについてもテストが考えられます²。恐らくですが、近年のコンピュータにとって500件やそこらのテストは大した負荷では無かろうという考えもあって、512bitまでの長さは全て用意したのでしょう。

そこから先は長さ611bitから51200bitまで99bit刻みで約2000件のテストや、入力メッセージの長さは固定で値だけランダムに振ったテストが100件、さらにbit単位の入力ではなくByte単位の入力に対するテストも用意されています。残念ながらCAVPのサイトには細かい理由までは記載されていませんが、どうしてこのような組み合わせが用意されたのか考えてみるのも面白いかもしれません。

他のアルゴリズムについて

CAVPでテストベクタが整備されているのは、CAVPを整備しているNIST（米国立標準技術研究所。暗号関係の標準を公開している）が推奨している（あるいは過去に推奨していた）もの³に限られます。

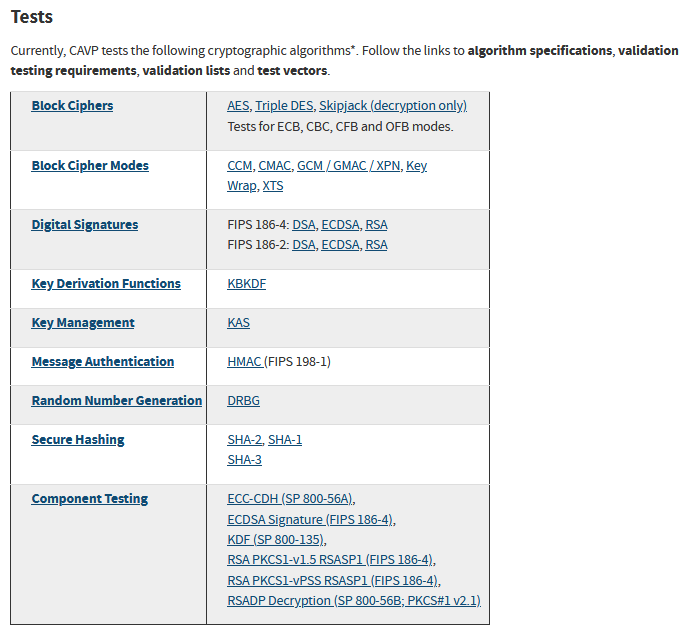
図. CAVP, Cryptographic Algorithm Validation Program （参照 2020年12月）より引用

では、CAVPに掲載されていないアルゴリズムを採用する場合はどうしましょうか？

アルゴリズムによっては他の情報源からテストベクタが公開されている場合があります。例えばRC4ならRFC6229ですね。ある程度メジャーなアルゴリズムであれば信頼できる情報源が得られるかもしれません。また、アルゴリズムの開発元や公開元へ問い合わせればテストベクタを提供してもらえる可能性があります。

ただし、信頼できる情報源が無いとか、貧弱なテストベクタ（件数や組み合わせが少なくてテストすべき組み合わせが欠けているデータ）しか得られない場合は注意が必要です。信頼できるテストベクタが入手できる他のアルゴリズムで代替できないか、乗り換えを検討してみるのも良いでしょう。

もう一つ意識しておきたいのは、テストベクタは簡単に作れるものではない、ということです。正解データを作れる環境を用意するだけでなく、対象のアルゴリズムやプログラミング言語やコンピュータアーキテクチャなどの仕様に明るく、不具合を引き起こしそうな（＝テストすべき）データ列の組み合わせを考えられる人が必要です。

認証制度

暗号モジュール製品の中には認証を取っているものがあります。日本で言うとIPA（独立行政法人情報処理推進機構）が運用するJCMVPが有名です。日本の電子政府推奨暗号リスト（CRYPTREC）掲載の暗号アルゴリズムなどを実装した暗号モジュールに対する第三者評価を行ってくれます。

入出力試験があるだけでなく鍵管理や関連文書についても評価されるため、本稿の主題からは少し外れますが、自前で品質を確保するのが難しい場合は認証取得済み製品を購入するのも良いでしょう。公式サイトに取得製品リストが掲載されています。

逆に、自社で暗号を用いた製品を作る方が品質を客観的に示したい場合には、認証取得を検討しても良いかもしれません。

おわりに

暗号モジュールをテストする難しさと、テストベクタについて紹介しました。

暗号アルゴリズムによっては規格ドキュメントにサンプルコードや動作確認用の入出力データが掲載されていることもありますが、往々にして付属の入出力データは件数が少なく、それだけを頼りに開発を終えてしまうと思わぬバグを残してしまうことがあります。

本文中で例に挙げたSHA-1についても、RFC3174内に仕様やサンプルコードとともにテストベクタが含まれているのですが、たったの4通りしかありません。CAVPにある数千件のテストベクタと比較すると、非常に頼りないと言えます。

本稿が暗号モジュールをテストする場合やアルゴリズムを選定する場合の参考になれば幸いです。

参考文献と参考Webサイト

CAVP, Cryptographic Algorithm Validation Program (https://csrc.nist.gov/projects/cryptographic-algorithm-validation-program)

RFC3174, US Secure Hash Algorithm (SHA-1) (https://tools.ietf.org/html/rfc3174)

RFC6229, Test Vectors for the Stream Cipher RC4 (https://tools.ietf.org/html/rfc6229)

JCMVP, 暗号モジュール試験及び認証制度 (https://www.ipa.go.jp/security/jcmvp/index.html)