オブジェクトの広場はオージス総研グループのエンジニアによる技術発表サイトです

AI

はじめての自然言語処理

第24回 SNGP による不確実性を考慮した文章分類
オージス総研 技術部 データエンジニアリングセンター
鵜野 和也
2022年12月22日

今回は SNGP を使って不確実性を考慮した文章分類を行います。「不確実性を考慮した」というのは、「どの分類か分からないデータ」に対しては「分からない」と答えるようにしたいということです。実際に SNGP を組み込んだモデルを作って素の BERT の分類モデルと比べてみましょう。

1. はじめに

今回は SNGP(Spectral-normalized Neural Gaussian Process)1 を使って不確実性を考慮した文章分類を行います。

BERT に SNGP を組み込んた文章分類モデルについては Tensorflow のチュートリアルがあります2。本記事もこのチュートリアルの内容に補足説明を入れつつ、 日本語のデータで動くように改修したものになっていますので、合わせて参考にして頂くと良いかと思います。

さて、BERT で普通に文章分類モデルを作ると、学習時に未経験のどの分類にも当てはまらないようなデータに対しても、高い確信度で「コレでしょ！」と回答する傾向があるように感じます。確信度に閾値を適用して、当てにならなさそうな推論結果を判別したいところですが、高い確信度で自信ありげに間違ってくれるので、どうにも上手くいきません。

この悩みに比較的シンプルな方法で対応できるのが、SNGP になります。

二値分類における予測不確実性を ResNet(左） とそれに SNGP を適用したもの（右）で比較すると以下のようになります。

uncertainty

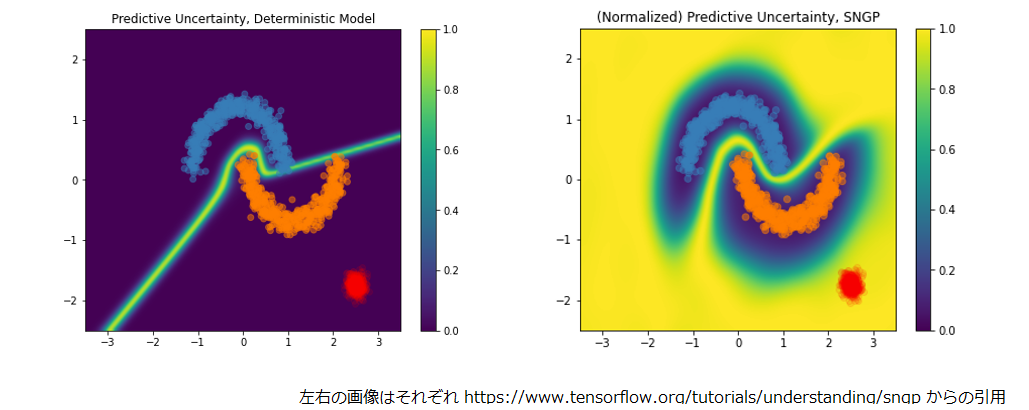
青とオレンジは学習データの分布、赤は学習時に未経験のデータ、背景色の黄色は予想が不確実（濃紺はその反対）とモデルが判断したことを示しています。

学習時に未経験であり、学習時のデータとは異なる分布の赤に対して ResNet（左）は自信をもって「これ、オレンジでしょ！」と判定していますが、SNGP を適用したほう（右）は「これ、よくわからないです。。。」と反応しているのが分かりますね。

それでは、まず SNGP についてご説明します。

2. SNGP

SNGP は残差接続のある深い隠れ層（残差付き隠れ層）に出力層を繋いだ分類モデルが話の前提になります。BERT の分類モデルもそんな感じですよね。この前提に SNGP を適用する場合の変更点は以下のようになります。

sngp

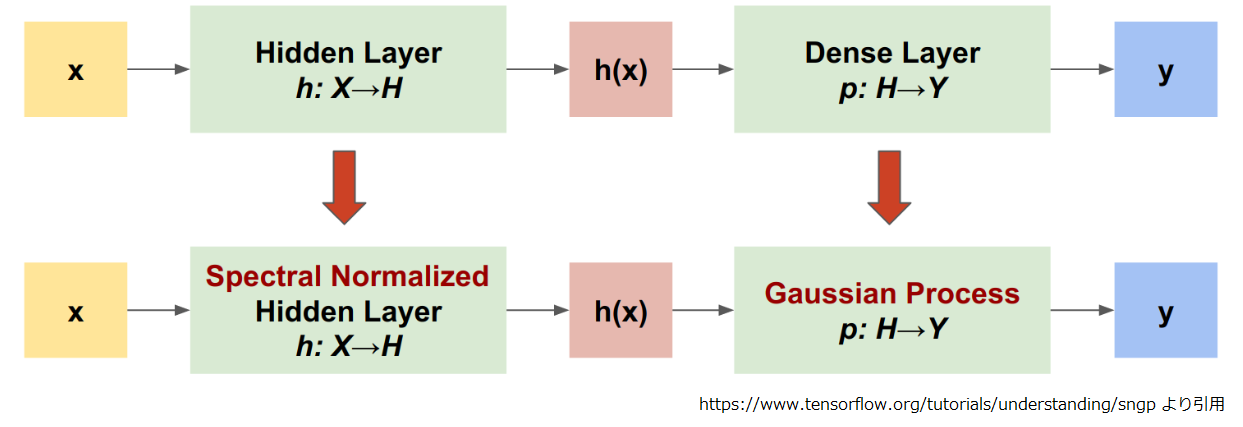
  • 残差付き隠れ層から出力される特徴量 H がネットワークへの入力である X の距離特徴を維持できるようにする為、残差付き隠れ層の重みにスぺクトル正規化を適用する。

  • 出力層 p:H→Y が投入されるデータの距離を認識できるよう、出力層を RBF カーネルのガウス過程(GP)に置き換え、この事後分散が入力 H の特徴量空間における学習データからの L2 距離で特徴づけられるようにする。

うーん、イマイチ良くわからないですね。もう少しくだけた言い回しにしましょう。

  • 一つ目は ネットワークへの入力を X とすると、X にもいろんな値があります。仮に x1, x2 があったとすると、この二つの距離感が「残差接続のある深い隠れ層」を通り抜けて出力された h1, h2 の距離感に反映されるようにします。 ということです。次の出力層での工夫がキモなのですが、そこにたどり着くまでに距離感の情報が消えていると、どうしようもないですからね。

  • 二つ目は 出力層から logit のスカラー値ではなく、平均がこう、分散がこうといった確率分布が出力されるようにして、学習データとかけ離れたデータを投入されると、出力される logit の分散が大きくなるようにします。 ということです。

logit の分散が大きければ「モデルは logit の値に自信を持っていない」ということなので、それを分類の確信度に反映させれば良いわけです。なんとなく、うまくいきそうな気がしますね。

順序逆になりますが、まずは出力層のガウス過程への換装から見ていきましょう。

ただ、まともに説明すると内容や分量が本連載の趣旨3から外れそうなので、論文1の数式をつまみ食いしながら雰囲気が伝われば、くらいで行きたいと思います。

3. ガウス過程

ガウス過程について一言で説明すると関数をサンプリングできる確率分布です。ここでは残差隠れ層からの出力 h を logit にする関数をサンプリングする感じですね。

N 件の学習データを D = {yi, xi}i=1N、残差隠れ層からの出力 hi = h(xi) が与えられたとして、 ガウス過程出力層 gN×1 = [g(h1),…,g(hN)]T の事前分布を以下の多変量ガウス分布としています。

gp_priori

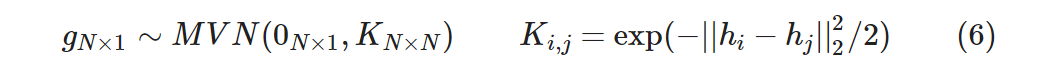
これは変数 N 個の多変量ガウス分布ですね。Ki,j が RBF カーネルで二点 i, j の距離が近ければ 1, 遠ければ 0 に近くなります。

ここで「h を logit にする関数をサンプリングするのに変数 N 個ってどういうこと？」となった人がいるかもしれません。 本来は学習データ D の N 個のサンプルの隙間にもデータは存在するはずで、それを考えると無限次元になるのですが、ここはサンプルのある N 個に着目してると思って下さい。

ただ、このままでは解析的にも計算量的にも厳しいので、以下のようにして低ランク近似します。

lowrank_approximation

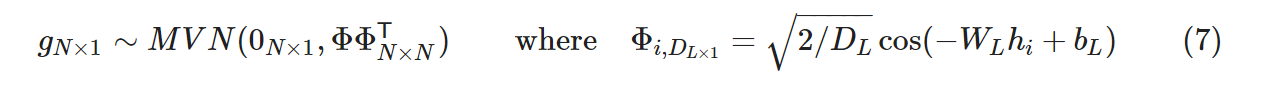
ここで各記号の意味合いですが以下のようになります。

  • Φi は DL 次元の最終層
  • hi=h(xi) は DL-1 次元の最終の直前の層
  • WL は [DL×DL-1] の固定の重み行列で各要素は N(0,1) から i.i.d でサンプリングされる。
  • bL は [DL×1] の固定のバイアスで各要素は Uniform(0,2π) から i.i.d でサンプリングされる。

いきなり cos やらサンプリングした固定の重みやら出てきて、「もう、何が何やら。。。」という感じです。 少し落ち着いて、感覚的に意味合いを考えて見ましょう。

近似の前後で平均は 0N×1 で変わりないですね。変わったのは共分散行列のほうです。 ようするに DL次元のベクトル Φi と Φj の内積が Ki,j の近似になるということで良さそうです。

この Φi は乱択化フーリエ特徴4と呼ばれるものです。

4. 乱択化フーリエ特徴

Φi ですが、意味合い的には直前層が出力した特徴量 hi の各次元の要素を次元毎にランダムに引いた直線上に写像して cos を採ったものになります。

ここで特徴量 hi のある 1 次元に着目して考えると以下のようになります。引かれた直線上に写像された点が cos で右側の単位円の円周上に写像されます。 このとき、直線上の点の高さが円周上を周回する角度になる訳ですね。

random_fourie_feature

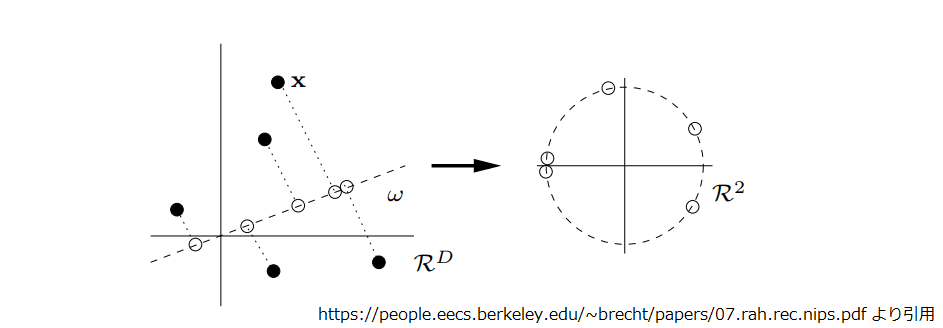
ここで二点 i,j の乱択化フーリエ特徴量Φi, Φjの内積は同じ次元の要素同士を掛け合わせた合計なので、 円周上に写像された二点が上下に分けた半円の同じ側にいれば内積に＋、異なる半円に分かれればーの寄与になります。

二点 i, j の特徴量 hi, hj が十分に近ければ、写像された円周上でも同一周回の近い位置になるはずで、高い確率で同じ半円に入るこになります。 hi, hj が遠ければ円周上で近いか遠いかは乱択化フーリエ特徴量のパラメータ次第となり、円周の反対側かもしれないし、周回違いで円周上の同じ場所にいるかもしれません。上下に分けた半円の同じ側にいるかどうか、つまり内積に＋の寄与かーの寄与かも乱択したパラメータ次第になります。

ただし Φ は DL 次元なので、1次元で見ると「近ければ内積に＋の寄与、遠ければ＋かーかわからない」ですが、 DL 次元を合計すれば、「遠ければ＋かーかわからない」の部分が平均化されて 0 になります。結局、元々の二点 i, j が「近ければ大きく、遠ければ小さい」ことになり、近似前の Ki,j が持っていた性質を近似出来ていることがわかります。

5. ニューラルネットによる表現

さて、ガウス過程の事前分布を乱択化フーリエ特徴量で低ランク近似しました。 これにより分類数 K (1≦k≦K) の分類問題の k 個目の logit を以下のニューラルネットで記述出来るようになりました。

logit

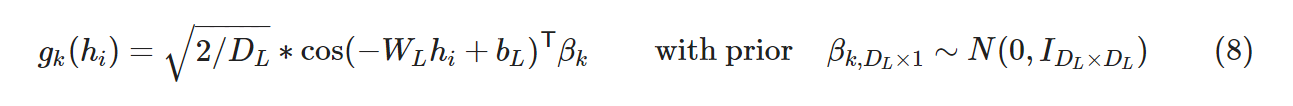
ここで各記号は以下のとおりです。

  • WL, bL : 前述の固定の重み
  • βk : 学習可能なパラメータで [DL×1] の形です。

gk(hi) は乱択化フーリエ特徴と βk を掛け合わたスカラー値です。これを logit と見なして学習する、ということで良いかと思います。

βk には事前分布が与えられてますから、ガウス線形モデルですね。つまり βk を確率分布として扱うことで、βk の値を決め打ちするのではなく、「このデータなら βk の自信度はこのくらい」という幅を持たせるようにしようということです。そして、ガウス線形モデルの学習というのは βk の事後分布 p(βk|D) を求めることです。

ここからは βk の事後分布 p(βk|D) 、つまり学習データ D を踏まえるとパラメータ βk がどうなるか?という話について考えていきます。

6. ラプラス近似による βk の事後分布

βk の事後分布の求め方については色々と方法はあるようですが、SNGP では βk の事後分布を得るのにラプラス近似5を使っています。ラプラス近似の説明や途中の計算は潔くすっ飛ばしてしまいますが、一言で言うと確率密度関数をガウス分布で近似するもので、 p(βk|D) の場合、以下のような βk の最大事後確率推定を中心とした DL 次元の多変量ガウス分布になります。

laplace_approx

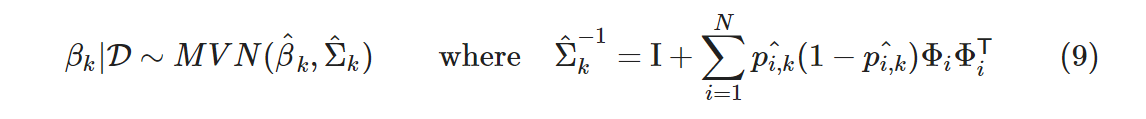
ここで各記号は以下のとおりです。

  • β^k : β^ = {β^k}k=1K で β^ は βの最大事後確率(MAP)推定、 argmaxβp(β|D) です。
  • p^i,k : β^の元での分類モデルの推定、 softmax(g^i) です。

β^ が求まれば、p^i,k も計算できるので、Σ^kも大丈夫そうですね。

そこで最大事後確率推定である β^ の求め方です。ようするに p(β|D) を最大化したい訳ですが、p(β|D) は以下のようになるので、

updating_beta

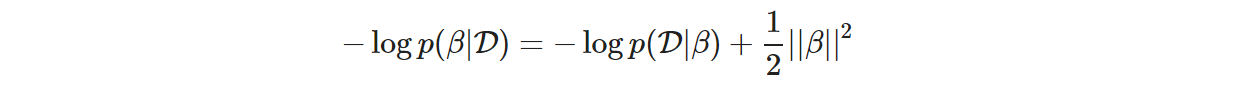
上式の右辺に関して勾配降下で更新すればＯＫとのことです。ここで -log p(D|β) は負の対数尤度、つまりクロスエントロピー誤差です。

ここまでが学習時に行う処理になります。論文にアルゴリズムの全体像が記載されていますが、ちょうど左半分まで来たところです。

algorithm

「あれ、そもそも β の確率分布が欲しかったんだっけ？」となりそうですが、それはアルゴリズムの右半分、推論時の処理になります。

7. 推論時の処理

学習時に β^ と Σ^k が計算できました。これらを使って推論していきます。

上記の Algorithm 2 のステップ 2 でテストサンプル x の乱択化フーリエ特徴を求め、ステップ 3 で学習済みパラメータ β と掛け合わせて logit (の平均) を求めます。ここまで学習時と同じですね。

同ステップ 4 で logit の分散を以下の数式で求めます。

post_var

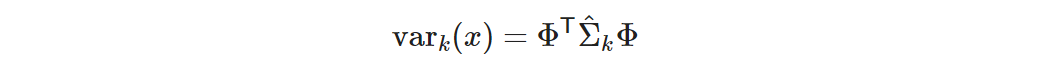
x の乱択化フーリエ特徴 Φ が [DL×1] で βk の共分散行列 Σ^k が [DL×DL] なのでスカラー値です。

分散の計算について補足

ちょうど Wikipedia の分散共分散行列のページ6にある、"線形作用素として“の項にある計算ですね。確率変数 X, Y があった時、その共分散 cov(X, Y) は以下のとおりです。

cov

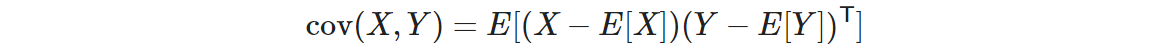
そして、ベクトル c, d があり確率変数 X の共分散行列が Σ だとすると、以下が成り立ちます。

as_linear_operator

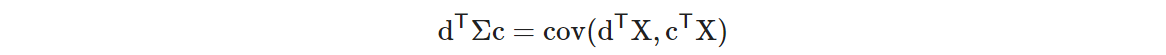
これを vark(x) に当てはめると、

var

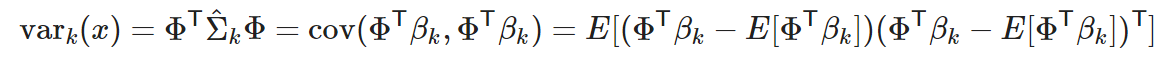
ΦTβk は logit ですから、確かに logit の分散が計算出来ていることが分かります。

ちなみに推論時にバッチサイズ B で処理すると vark(x) が [B, B] の共分散行列になります。例えば B = 3 として、 σ2m,n を ΦmTβ と ΦnTβ の共分散とすると、以下のような感じになると思います。

batch_prediction

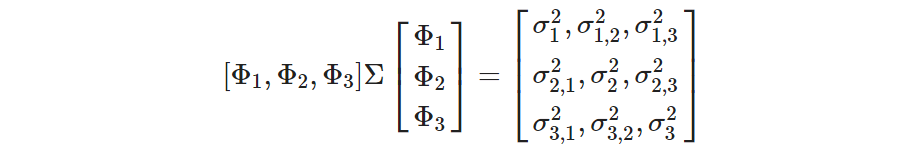
各サンプルの分散だけ欲しければ、対角成分をとればＯＫです。

事後予測確率の計算

ようやく分類の確信度を計算するところまできました。前述の Algorithm 2 では logit の確率分布を積分してますが、 Tensorflow の実装7では平均場近似8を使って以下のように計算しています。

mean_field_approx

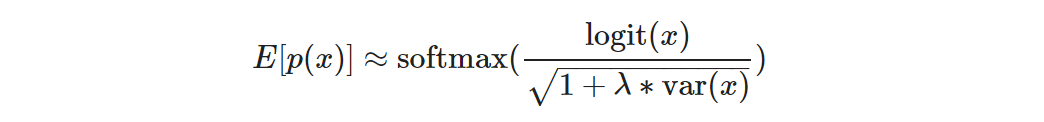
ここで λ はハイパーパラメータです。上式の形になる過程の話は飛ばしますが、感覚的には分散が大きくなると softmax への入力が小さくなりますね。

以下のように softmax は入力値が小さくなると、その比率は同じでも出力される確信度は平滑化されていきます。

softmax

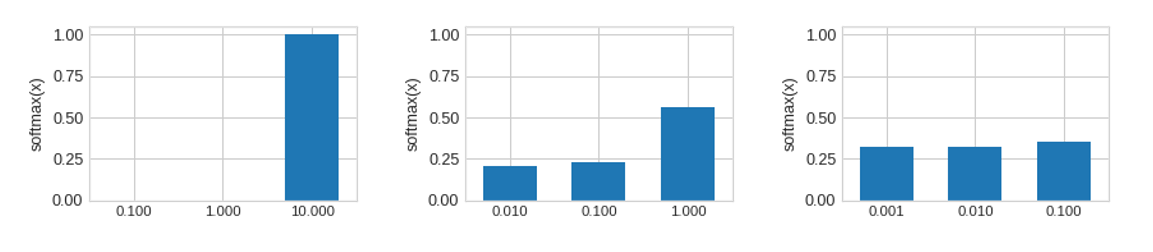
つまり、SNGP では学習データから乖離した推論データを投入されると、logit の分散が大きくなり、結果として出力される確信度が一様分布に近くなることが分かります。

話が長くなり忘れかけていましたが、SNGP の "SN” の話も少しだけしておきましょう。

8. 残差付き隠れ層のスぺクトル正規化

後回しにしてましたが残差付き隠れ層で入力の距離特徴を維持できるようにする件です。

ResNet や Transformer のようなモデルは以下のような構造をしています。

residual_network

論文1によると、全ての非線形残差写像 {gl}l=1L-1においてリプシッツ定数9を 1 以下にすることで距離特徴を維持できるようになるとのことです。

リプシッツ定数について補足しておくと、以下のように X 印が関数上の点をポイントしながら並行移動したとき、関数の値が常に X の薄緑色の部分に入れば、関数はリプシッツ連続で X の傾きがリプシッツ定数です。感覚的には変化の度合いに制約がかかる感じですね。

lipschitz_continuity

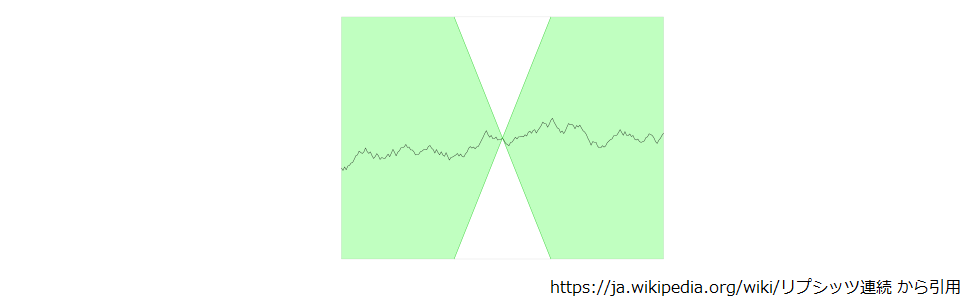
さらに非線形残差写像 gl(x) = σ(Wlx + bl) 、とすると、

lipschitz_constraint

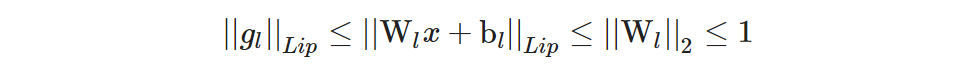
になるそうなので、Wl のスペクトルノルム（最大の特異値）||Wl||2 に以下の制約をかけることで間接的に距離特徴の維持が可能になります。これがスぺクトル正規化で、前述の Algorithm 1 のステップ 5 の計算になります。

spectral normalization

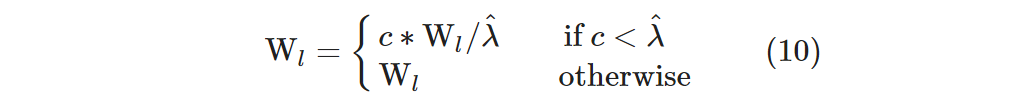
ここで各記号は以下のとおりです。

  • λ^ : 学習ステップの最初にべき乗法で計算するスペクトルノルムの見積もり。 λ≈ ||Wl||2。
  • c : ||Wl||2 ≤ c に制約するハイパーパラメータ。

それでは BERT の文章分類に SNGP を適用して効果の有無を見てみることにしましょう。

9. 環境のセットアップ

ここからは実際にコードを動かしながら SNGP の学習を行ってみます。今回も Colab で動かす想定でコードスニペットを入れていくので、 新たにノートブックを開き、アクセラレータは GPU を選んでおいて下さい。

まずは tensorflow-text と tf-models-official をインストールします。

!pip install tf-models-official==2.8.0
!pip install tensorflow-text==2.8.2

筆者が試したタイミングではチュートリアル2のとおりに nightly を入れると cuDNN でエラーになりました。 筆者が動作確認した時点でのバージョンの組み合わせは以下のとおりです。

!pip list | grep -e tensorflow -e tf-
# tensorflow                    2.8.2+zzzcolab20220719082949
# tensorflow-addons             0.17.1
# tensorflow-datasets           4.0.1
# tensorflow-estimator          2.8.0
# tensorflow-gcs-config         2.8.0
# tensorflow-hub                0.12.0
# tensorflow-io-gcs-filesystem  0.26.0
# tensorflow-metadata           1.9.0
# tensorflow-model-optimization 0.7.3
# tensorflow-probability        0.16.0
# tensorflow-text               2.8.2
# tf-models-official            2.8.0
# tf-slim                       1.1.0

トークナイザと事前学習済みモデルは transformers のものを使いました。 MeCab も入れておきます。

!pip install transformers
!apt-get install mecab mecab-ipadic-utf8 python-mecab libmecab-dev
!pip install mecab-python3 fugashi ipadic

10. 事前学習済みモデルを Keras の BERT 実装にロード

SNGP の実装は Tensorflow の Keras API で実装されているので、まずは transformers で公開されている事前学習モデルのパラメータを Keras の BERT 実装に組み込むところから始めましょう。

まずは、いつも使っている東北大さんのモデルからパラメータを state_dict の形で取り出します。

from transformers import BertModel
model = BertModel.from_pretrained('cl-tohoku/bert-base-japanese-whole-word-masking')
state_dict = model.state_dict()

次に Keras の BERT をロードして初期化し、パラメータを取り出します。

BertEncoderV2 に type_vocab_size=2 を指定するのがポイントですね。これでオリジナルの BERT や transformers で token_type_ids と呼ばれるモノのサイズを指定します。デフォルトが 16 なのですが、これを東北大さんのモデルに合わせて 2 にしておきます。

import tensorflow as tf
from official.nlp.modeling.networks.bert_encoder import BertEncoderV2

bert = BertEncoderV2(vocab_size=32000, type_vocab_size=2)

input_word_ids = tf.keras.layers.Input(shape=(None,), dtype=tf.int32, name='input_word_ids')
input_mask = tf.keras.layers.Input(shape=(None,), dtype=tf.int32, name='input_mask')
input_type_ids = tf.keras.layers.Input(shape=(None,), dtype=tf.int32, name='input_type_ids')
inputs = {
    "input_word_ids": input_word_ids,
    "input_mask": input_mask,
    "input_type_ids": input_type_ids    
}

outputs = bert.call(inputs)

bert_variables = []
for v in bert.variables:
  bert_variables.append([v.name, v])

transformers 側のパラメータの数をチェックしておきます。

len(state_dict)
# 200

続いて Keras の BERT です。

len(bert_variables)
# 199

Keras 側が 1 つ少ないですが、確認してみると “embeddings.position_ids” という [1, 512] のパラメータでした。中身を見ると 0 ～ 511 の連番が入ってるだけだったので、今回は無視することにしました。

ここからはパラメータ名とシェイプを変換します。まずは transformers 側のパラメータ名に対するマッチングパターンです。

torch_param_names='''
encoder.layer.([0-9]*).intermediate.dense.weight
encoder.layer.([0-9]*).intermediate.dense.bias
encoder.layer.([0-9]*).output.dense.weight
encoder.layer.([0-9]*).output.dense.bias
encoder.layer.([0-9]*).output.LayerNorm.weight
encoder.layer.([0-9]*).output.LayerNorm.bias
encoder.layer.([0-9]*).attention.self.query.weight
encoder.layer.([0-9]*).attention.self.query.bias
encoder.layer.([0-9]*).attention.self.key.weight
encoder.layer.([0-9]*).attention.self.key.bias
encoder.layer.([0-9]*).attention.self.value.weight
encoder.layer.([0-9]*).attention.self.value.bias
encoder.layer.([0-9]*).attention.output.dense.weight
encoder.layer.([0-9]*).attention.output.dense.bias
encoder.layer.([0-9]*).attention.output.LayerNorm.weight
encoder.layer.([0-9]*).attention.output.LayerNorm.bias
embeddings.word_embeddings.weight
embeddings.position_embeddings.weight
embeddings.token_type_embeddings.weight
embeddings.LayerNorm.weight
embeddings.LayerNorm.bias
pooler.dense.weight
pooler.dense.bias
'''
torch_param_names = [name for name in torch_param_names.split("\n") if len(name) > 0]

次は上記のパターンにマッチした場合の変更ルールです。

keras_param_names='''
transformer/layer_\\1/intermediate/kernel:0
transformer/layer_\\1/intermediate/bias:0
transformer/layer_\\1/output/kernel:0
transformer/layer_\\1/output/bias:0
transformer/layer_\\1/output_layer_norm/gamma:0
transformer/layer_\\1/output_layer_norm/beta:0
transformer/layer_\\1/self_attention/query/kernel:0
transformer/layer_\\1/self_attention/query/bias:0
transformer/layer_\\1/self_attention/key/kernel:0
transformer/layer_\\1/self_attention/key/bias:0
transformer/layer_\\1/self_attention/value/kernel:0
transformer/layer_\\1/self_attention/value/bias:0
transformer/layer_\\1/self_attention/attention_output/kernel:0
transformer/layer_\\1/self_attention/attention_output/bias:0
transformer/layer_\\1/self_attention_layer_norm/gamma:0
transformer/layer_\\1/self_attention_layer_norm/beta:0
word_embeddings/embeddings:0
position_embedding/embeddings:0
type_embeddings/embeddings:0
embeddings/layer_norm/gamma:0
embeddings/layer_norm/beta:0
pooler_transform/kernel:0
pooler_transform/bias:0
'''
keras_param_names = [name for name in keras_param_names.split("\n") if len(name) > 0]

定義したパターンを使ったパラメータ名書き換え関数です。

import re
def translate_variable_name(org):
  for pattern, target in zip(torch_param_names, keras_param_names):
    translated = re.sub(pattern, target, org)
    if org != translated:
      return translated

試してみましょう。大丈夫そうですね。

translate_variable_name("encoder.layer.11.intermediate.dense.weight")
# transformer/layer_11/intermediate/kernel:0

次にシェイプの書き換え関数です。基本的には reshape で形を合わせるだけで OK なのですが、 transformers 側が [768, 768] の形の時に転置を挟むのがポイントになります。

import numpy as np
def convert_shape(name, array, target_shape):
  org_shape = list(array.shape)
  if org_shape == target_shape:
    return array
  if org_shape == [768, 768]:
    array = np.transpose(array)
  if (org_shape == [12, 64] and target_shape == [768]) or (
     org_shape == [768] and target_shape == [12, 64]) or (  
     org_shape == [768, 768] and target_shape == [12, 64, 768]) or ( 
     org_shape == [768, 768] and target_shape == [768, 12, 64]) or (
     org_shape == [768, 12, 64] and target_shape == [768, 768]) or (
     org_shape == [12, 64, 768] and target_shape == [768, 768]):
    converted = np.reshape(array, target_shape)
    print("{}:{} => {}".format(name, org_shape, list(converted.shape)))
    return converted
  elif (org_shape == [3072, 768] and target_shape == [768, 3072]) or (
        org_shape == [768, 3072] and target_shape == [3072, 768]):
    converted = np.transpose(array)
    print("{}:{} => {}".format(name, org_shape, list(converted.shape)))
    return converted
  else:
    message= "Unknown conversion : {}:{} => {}".format(name, org_shape, target_shape)
    raise Exception(message)

以下のようにしてパラメータを変換します。

def find_bert_variable(query):
  for name, variable in bert_variables:
    if query == name:
      return variable

translated = []
for name, tensor in state_dict.items():
  target_name = translate_variable_name(name)
  if target_name is None:
    continue
  target_variable = find_bert_variable(target_name)
  target_array = convert_shape(target_name, np.array(tensor), target_variable.shape.as_list())
  translated.append([target_name, target_array])

# transformer/layer_0/self_attention/query/kernel:0:[768, 768] => [768, 12, 64]
# transformer/layer_0/self_attention/query/bias:0:[768] => [12, 64]
# transformer/layer_0/self_attention/key/kernel:0:[768, 768] => [768, 12, 64]
# ...

変換したパラメータを Keras の BERT 実装に上書きします。

def find_translated_variable(query):
  for name, variable in translated:
    if query == name:
      return variable

for name, variable in bert_variables:
  translated_value = find_translated_variable(name)
  variable.assign(translated_value)

11. データセットの準備

データセットはこの連載で何度か使っている livedoor News コーパス(以下、LDCCと記述)の文章分類を題材にします。

LDCC は以前に TSV の形に加工済みのものを使いました。（加工の仕方は忘れてしまいました。。。）

!gsutil cp gs://somewhere/ldcc/[dt]*.tsv .
# Copying gs://somewhere/ldcc/dev.tsv...
# Copying gs://somewhere/ldcc/test.tsv...
# Copying gs://somewhere/ldcc/train.tsv...
# / [3 files][ 24.0 MiB/ 24.0 MiB]                                                
# Operation completed over 3 objects/24.0 MiB.

TSV ファイルの中身は以下のような感じです。

!head -5 train.tsv
# label text
# movie-enter   大島優子がここからどう破滅していくのか？　『闇金ウシジマくん』特報解禁“闇金”という禁断の題材をリアルに描いた漫画史上最大の問題作「闇金ウシジマくん」が、映画化され8月25日から公開
# movie-enter   インタビュー：クリスチャン・ベール「演じることができるのは役者だけ」公開当時、全米歴代2位というメガヒットを記録し、世界中で社会現象を巻き起こした『ダークナイト』から4年、「誰もが
# kaden-channel ブラックマジックデザイン、HyperDeck SSD レコーダーに タイムコード、DNxHD QuickTime サポートを追加【ビデオSALON】ブラックマジックデザインはHyperDeck 2.5 パブリックベータ版をリリ
# kaden-channel センター試験終了！　受験生ファンに眞鍋かをりが的確なアドバイスをしていた【話題】寒い週末、毎年恒例のセンター試験が行われていた。受験生にとっては大切な日。ファンの受験をタレントの

TSV をロードしてトークナイズする関数です。

from transformers import BertJapaneseTokenizer
tokenizer = BertJapaneseTokenizer.from_pretrained('cl-tohoku/bert-base-japanese-whole-word-masking')

import numpy as np
def load_tsv(fname, tokenizer, label_map=None):
  with open(fname, "r") as f:
    lines = f.readlines()
    lines = [line.strip().split("\t") for line in lines[1:]]
    labels = [line[0] for line in lines]
    if not label_map:
      label_map = {l:i for i, l in enumerate(set(labels))}  
    labels = [label_map[label] for label in labels]
    texts = [line[1] for line in lines]
    features = tokenizer.batch_encode_plus(texts, max_length=512, padding="max_length", truncation=True, return_tensors="np")
    inputs = {
      "input_word_ids": features["input_ids"], 
      "input_mask": features["attention_mask"], 
      "input_type_ids": features["token_type_ids"], 
    }
    return inputs, np.array(labels), label_map

LDCC は本来 9 分類のデータセットですが、今回は sports-watch を OOD(Out-Of-Domain) データとして除外し、残りの 8 クラスで分類モデルを 作ります。

クラス名とインデックスのマッピングで sports-watch に -1 を設定し、

label_map = {
 'dokujo-tsushin': 0,
 'it-life-hack': 1,
 'kaden-channel': 2,
 'livedoor-homme': 3,
 'movie-enter': 4,
 'peachy': 5,
 'smax': 6,
 'topic-news': 7,
 'sports-watch': -1,    
}

TSV ファイルをロードして、

train_x, train_y, _= load_tsv("train.tsv", tokenizer, label_map)
dev_x, dev_y, _ = load_tsv("dev.tsv", tokenizer, label_map)
test_x, test_y, _ = load_tsv("test.tsv", tokenizer, label_map)

sports-watch (ラベルが -1) を除外したデータを作ります。

train_x_wo_ood = {key:np.array([v for l, v in zip(train_y, value) if l != -1]) for key, value in train_x.items()}
train_y_wo_ood = np.array([l for l in train_y if l != -1])
dev_x_wo_ood = {key:np.array([v for l, v in zip(dev_y, value) if l != -1]) for key, value in dev_x.items()}
dev_y_wo_ood = np.array([l for l in dev_y if l != -1])
test_x_wo_ood = {key:np.array([v for l, v in zip(test_y, value) if l != -1]) for key, value in test_x.items()}
test_y_wo_ood = np.array([l for l in test_y if l != -1])

学習データは 3888 件になりました。

train_y_wo_ood.shape
(3888,)

12. SNGP-BERT

ここから BERT に SNGP を適用した分類器を準備していきます。

まずは、普通の BERT の分類器です。

import numpy as np
import tensorflow as tf
import official.nlp.modeling.layers as layers
import official.nlp.optimization as optimization

class BertClassifier(tf.keras.Model):
  def __init__(self, bert_encoder, 
               num_classes=150, inner_dim=768, dropout_rate=0.1,
               **classifier_kwargs):

    super().__init__()
    self.classifier_kwargs = classifier_kwargs
    self.bert_encoder = bert_encoder
    self.classifier = self.make_classification_head(num_classes, inner_dim, dropout_rate)

  def make_classification_head(self, num_classes, inner_dim, dropout_rate):
    return layers.ClassificationHead(
        num_classes=num_classes, 
        inner_dim=inner_dim,
        dropout_rate=dropout_rate,
        **self.classifier_kwargs)

  def call(self, inputs, **kwargs):
    encoder_outputs = self.bert_encoder(inputs)
    classifier_inputs = encoder_outputs['sequence_output']
    return self.classifier(classifier_inputs, **kwargs)

続いて SNGP を適用した分類器です。 平均場近似の λ に相当する temperature には何度か試した結果、50 を設定しました。

class ResetCovarianceCallback(tf.keras.callbacks.Callback):
  def on_epoch_begin(self, epoch, logs=None):
    """Resets covariance matrix at the begining of the epoch."""
    if epoch > 0:
      self.model.classifier.reset_covariance_matrix()

class SNGPBertClassifier(BertClassifier):

  def make_classification_head(self, num_classes, inner_dim, dropout_rate):
    print("num_classes={}, inner_dim={}, dropout_rate={}".format(num_classes, inner_dim, dropout_rate))
    return layers.GaussianProcessClassificationHead(
        num_classes=num_classes, 
        inner_dim=inner_dim,
        dropout_rate=dropout_rate,
        gp_cov_momentum=-1,
        temperature=50.,
        **self.classifier_kwargs)

  def fit(self, *args, **kwargs):
    """Adds ResetCovarianceCallback to model callbacks."""
    kwargs['callbacks'] = list(kwargs.get('callbacks', []))
    kwargs['callbacks'].append(ResetCovarianceCallback())

    return super().fit(*args, **kwargs)

ResetCovarianceCallback は学習中に共分散行列を計算する際、単一サンプルを複数回カウントすることを回避する為のコールバックです。 エポックの開始タイミングでカウントをリセットする作りなので、 Early Stopping を使うとカウントが中途半端になってしまうところは注意が必要ですね。

SNGPBertClassifier に関しては、前述のコールバックを組み込み、分類のヘッドを SNGP を実装した GaussianProcessClassificationHead に差し替えた以外は変更ありません。

GaussianProcessClassificationHead の実装はだいたい論文1のとおりのようですが、β や Σ がクラス毎ではなく全クラス共通になっているので、そこだけ注意して下さい。

そうそう、このコードを見て「え、ちょっと待って！」となった人がいるかもしれないので補足します。

スペクトル正規化の適用箇所

スペクトル正規化の説明のところで、「全ての非線形残差写像 {gl}l=1L-1においてリプシッツ定数9を 1 以下にすることで距離特徴を維持できる」と言っておきながら、BERT 本体はそのままで、分類のヘッドだけ差し替えてます。「どういうことだ？」と思って調べてみましたが、

論文1の Appendix C.2 (page. 22) に以下の記述がありました。

When using spectral normalization, we set the hyperparameter c = 0.95 and apply it to the pooler dense layer of the classification token. We do not spectral normalization to the hidden transformer layers, as we find the pre-trained BERT representation is already competent in preserving input distance due to the masked language modeling training, and further regularization may in fact harm its predictive and calibration performance.

事前学習済みの BERT は十分距離特徴を維持できてるから、分類ヘッドの全結合層だけスペクトル正規化しました、ということのようです。

13. 文章分類の学習

それでは学習をしてみましょう。

東北大さんのパラメータで初期化済みの bert を SNGP-BERT の分類器に組み込みます。

model = SNGPBertClassifier(bert, num_classes=len(label_map)-1) # "-1" is "sports-watch"
# num_classes=8, inner_dim=768, dropout_rate=0.1

エポック数やバッチサイズの設定です。

NUM_EXAMPLES = len(train_y_wo_ood)
TRAIN_EPOCHS = 3
TRAIN_BATCH_SIZE = 8
EVAL_BATCH_SIZE = 8

オプティマイザ、損失関数、メトリクス関数を用意します。

def bert_optimizer(learning_rate, train_data_size,
                   batch_size=TRAIN_BATCH_SIZE, epochs=TRAIN_EPOCHS, 
                   warmup_rate=0.1):
  """Creates an AdamWeightDecay optimizer with learning rate schedule."""

  steps_per_epoch = int(train_data_size / batch_size)
  num_train_steps = steps_per_epoch * epochs
  num_warmup_steps = int(warmup_rate * num_train_steps)  

  # Creates learning schedule.
  lr_schedule = tf.keras.optimizers.schedules.PolynomialDecay(
      initial_learning_rate=learning_rate,
      decay_steps=num_train_steps,
      end_learning_rate=0.0)  

  return optimization.AdamWeightDecay(
      learning_rate=lr_schedule,
      weight_decay_rate=0.01,
      epsilon=1e-6,
      exclude_from_weight_decay=['LayerNorm', 'layer_norm', 'bias'])

optimizer = bert_optimizer(learning_rate=1e-4, train_data_size=NUM_EXAMPLES)
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.metrics.SparseCategoricalAccuracy()

モデルをコンパイルして学習を開始します。

fit_configs = dict(batch_size=TRAIN_BATCH_SIZE,
                   epochs=TRAIN_EPOCHS,
                   validation_batch_size=EVAL_BATCH_SIZE, 
                   validation_data=(dev_x_wo_ood, dev_y_wo_ood))

model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
model.fit(train_x_wo_ood, train_y_wo_ood, **fit_configs)
# Epoch 1/3
# WARNING:tensorflow:Gradients do not exist for variables ['pooler_transform/kernel:0', 'pooler_transform/bias:0'] when minimizing the loss. If you're using `model.compile()`, did you forget to provide a `loss`argument?
# WARNING:tensorflow:Gradients do not exist for variables ['pooler_transform/kernel:0', 'pooler_transform/bias:0'] when minimizing the loss. If you're using `model.compile()`, did you forget to provide a `loss`argument?
# WARNING:tensorflow:Gradients do not exist for variables ['pooler_transform/kernel:0', 'pooler_transform/bias:0'] when minimizing the loss. If you're using `model.compile()`, did you forget to provide a `loss`argument?
# WARNING:tensorflow:Gradients do not exist for variables ['pooler_transform/kernel:0', 'pooler_transform/bias:0'] when minimizing the loss. If you're using `model.compile()`, did you forget to provide a `loss`argument?
# 486/486 [==============================] - 571s 1s/step - loss: 0.6698 - sparse_categorical_accuracy: 0.8048 - val_loss: 0.4152 - val_sparse_categorical_accuracy: 0.8974
# Epoch 2/3
# 486/486 [==============================] - 585s 1s/step - loss: 0.2656 - sparse_categorical_accuracy: 0.9442 - val_loss: 0.2096 - val_sparse_categorical_accuracy: 0.9460
# Epoch 3/3
# 486/486 [==============================] - 586s 1s/step - loss: 0.0637 - sparse_categorical_accuracy: 0.9838 - val_loss: 0.1240 - val_sparse_categorical_accuracy: 0.9691
# <keras.callbacks.History at 0x7f85142fed10>

検証データでの val_sparse_categorical_accuracy を見る限り、 SNGP によって精度劣化している様子はみられませんね。 モデルを SavedModel にして保存しておきましょう。

model.save("./keras_bert_sngp_ldcc_wo_ood")
# WARNING:absl:Found untraced functions such as word_embeddings_layer_call_fn, word_embeddings_layer_call_and_return_conditional_losses, position_embedding_layer_call_fn, position_embedding_layer_call_and_return_conditional_losses, type_embeddings_layer_call_fn while saving (showing 5 of 414). These functions will not be directly callable after loading.
# INFO:tensorflow:Assets written to: ./keras_bert_sngp_ldcc_wo_ood/assets
# INFO:tensorflow:Assets written to: ./keras_bert_sngp_ldcc_wo_ood/assets

なにやら警告が出ていて、保存した SavedModel は Keras のモデルではなくなってしまっているようです。 ただ、ロードして追加で学習することはできませんが、推論するには特に問題ないので、今回はこのままにしておきます。

14. OOD 性能の評価

学習したモデルを使って OOD 性能をみてみましょう。

先程の SavedModel をロードして、

import tensorflow as tf
saved_model = tf.saved_model.load("./keras_bert_sngp_ldcc_wo_ood")

ロードしたモデルで推論をする関数です。

import math
def batch(xs, ys, batch_size):
  xbs = []
  ybs = []
  num_batch = math.ceil(len(ys) / batch_size)
  for i in range(num_batch):
    head = i * batch_size
    tail = head + batch_size
    #print("head:{}, tail={}".format(head, tail))
    xb = {key:value[head:tail] for key, value in xs.items()}
    yb = ys[head:tail]
    xbs.append(xb)
    ybs.append(yb)
  return xbs, ybs

def oos_predict(model, test_x, test_y, **model_kwargs):
  oos_labels = []
  oos_probs = []
  xbs, ybs = batch(test_x, test_y, batch_size=EVAL_BATCH_SIZE)

  for xb, yb in zip(xbs, ybs): 
    pred_logits = model(xb, **model_kwargs)
    pred_probs_all = tf.nn.softmax(pred_logits, axis=-1)
    pred_probs = tf.reduce_max(pred_probs_all, axis=-1)
    oos_labels.append(yb)
    oos_probs.append(pred_probs)

  oos_probs = tf.concat(oos_probs, axis=0)
  oos_labels = tf.concat(oos_labels, axis=0) 

  return oos_probs, oos_labels

ラベルを再作成して、推論を実行します。

test_y_ood = np.array([0 if l != -1 else 1 for l in test_y])
sngp_probs, ood_labels = oos_predict(saved_model, test_x , test_y_ood)

ここで sngp_probs は全クラス中で最大の確信度、 ood_labels はデータが既知(sports-watch 以外)なら 0、OOD(sports-watch) なら 1 です。

OOD か否かで確信度に差があることが見て取れます。

probs_id = [p for p, l in zip(sngp_probs, ood_labels) if l == 0]
probs_od = [p for p, l in zip(sngp_probs, ood_labels) if l == 1]
print("Avg prob of in-domain  :{:.3f}".format((sum(probs_id)/len(probs_id)).numpy()))
print("Avg prob of out-domain :{:.3f}".format((sum(probs_od)/len(probs_od)).numpy()))
# Avg prob of in-domain  :0.927
# Avg prob of out-domain :0.627

チュートリアル2に倣い、サンプルが OOD である確率を “1 - 分類の確信度” として、キャリブレーション曲線を描くと以下のようになりましました。

ood_probs = 1 - sngp_probs

from sklearn.calibration import calibration_curve
prob_true, prob_pred = sklearn.calibration.calibration_curve(
    ood_labels, ood_probs, n_bins=20, strategy='quantile')

plt.plot(prob_pred, prob_true)

plt.plot([0., 1.], [0., 1.], c='k', linestyle="--")
plt.xlabel('Predictive Probability')
plt.ylabel('Predictive Accuracy')
plt.title('Calibration Plots, SNGP')

plt.show()

calibration

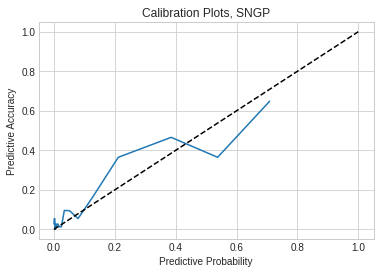
この曲線は対角線に近い程、良好な結果になります。このプロットだと不確実性が 0.38 (分類した確信度が 0.62) のとき、それが OOD のデータである確率が 0.47 という見方になります。

ただ上図だとプロット上の点がどの程度のサンプル数の集計によるのかが分かりにくいですね。 通常の BERT でも同様のモデルを作り、OOD、非OOD それぞれについて、観測された不確実性に関するサンプル数の分布を比較してみました。

bert_dist

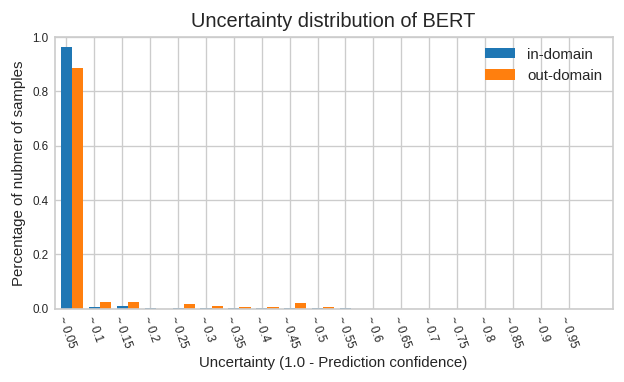
通常の BERT では OOD データの 90% 弱が不確実性 0.05 以下の範囲に含まれてしまうことが分かります。 言い換えると、OOD データであっても 9 割方は確信度 0.95 以上で「コレでしょ！」と判定してしまう訳です。

次は SNGP-BERT です。

sngp_dist

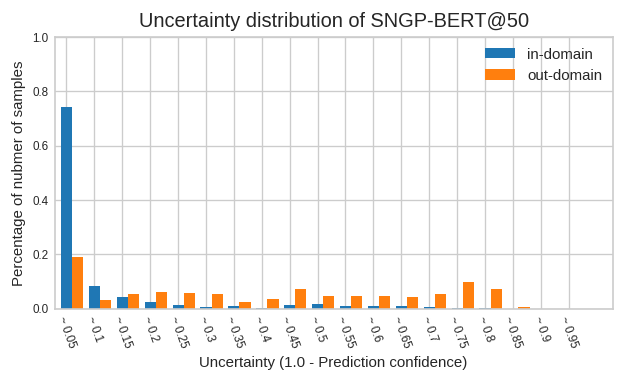
通常の BERT と比較して SNGP-BERT の方は 2 割弱が不確実性 0.05 以下の範囲に入るものの、その傾向はかなり低減されていることが分かります。

使用したデータセットによるものか、チュートリアル2で示された結果ほど綺麗な傾向は出せませんでしたが、 それなりの効果は望めそうなことは確認できたかと思います。

ただ非OODのデータに対する確信度も下がってるので分類精度に対する影響も確認しておきましょう。sports-watch を抜いたテストデータで推論して f1 スコアを比較しました。

f1_score

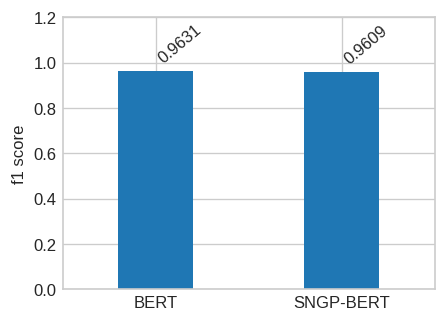
ほとんど同じです。これなら分類精度に対する影響は、ほぼないと考えてよさそうですね。

15. おわりに

今回は、SNGP を文章分類に適用してその効果を見てみました。出力層を差し替えるだけで効果が得られるのが良いですね。 次回は FasterTransformer を紹介したいと思います。BERT を試すといきなり妙な値が返ってきたり不穏なところもあったりしてますが、 大丈夫でしょうか。。。

  1. https://arxiv.org/abs/2006.10108 ↩

  2. https://www.tensorflow.org/text/tutorials/uncertainty_quantification_with_sngp_bert ↩

  3. この連載の数式は基本的に四則演算と指数・対数くらいでどうにかなるくらいのレベルで抑えて記述しています。筆者のキャパとも言えます。 ↩

  4. https://people.eecs.berkeley.edu/~brecht/papers/07.rah.rec.nips.pdf ↩

  5. https://masamunetogetoge.com/laplace-bayeslogistic  ↩

  6. https://ja.wikipedia.org/wiki/%E5%88%86%E6%95%A3%E5%85%B1%E5%88%86%E6%95%A3%E8%A1%8C%E5%88%97 ↩

  7. https://github.com/tensorflow/models/blob/a4ae812e57a14108870f295a9e87c5a5a9f2a73f/official/nlp/modeling/layers/gaussian_process.py#L459-L494 ↩

  8. https://arxiv.org/pdf/2006.07584.pdf ↩

  9. https://mathwords.net/lipschitz が分かりやすいでしょうか。このページにでてくる K あるいはその最小値がリプシッツ定数です。 ↩