オブジェクトの広場はオージス総研グループのエンジニアによる技術発表サイトです

クラウド/Webサービス

ビットコイン論文からさぐる ブロックチェーンのヒント

第11回 確率
オージス総研
樋口 匡俊
2019年12月25日

今回はビットコイン論文の第11章「Calculations」を読んでいきます。残る第12章「Conclusion」はまとめですので、本論としてはこの第11章が最後、そしてこの連載も今回が最終回です。

賭けはしなければならない

賭けの論理を用いて信仰を説く、「パンセ」の「パスカルの賭け」。その対話形式の断章の中に、以下のようなやりとりがあります。

「表が出るか、裏が出るかだ。きみはどちらに賭けるか。」
「正しいのは、賭けなどしないことだ。」
「そのとおりだ。だが、賭けはしなければならない。勝手にどうでもできるということではないのだ。もうきみは舟を乗り出しているのだ。」

ビットコインを使うということは、「パスカルの賭け」のように、ある種の賭けを迫られるということでもあります。ビットコインの基本となる仕組みには、いくつか偶然の要素が含まれているからです。

例えば第5回で、PoW は平均10分間に1度しか「アタリ」が出ないよう難易度が調整されると説明しました。しかし、平均はあくまで平均です。神がかった幸運の持ち主が、超高速に次々と「アタリ」を引き当てる可能性は、ごくごくわずかながら残っています。もしもそれが攻撃者であれば、いとも簡単に攻撃を成功させることができるでしょう。

今回読む第11章「Calculations」では、そんな賭けを迫られた人を想定し、確率論を用いた分析が行われています。

参考資料について

これまでのような文章と図による説明とはうってかわって、第11章には数式がいくつか出てきます。本記事では、数式の直観的な意味と考え方を紹介していきます。

数式の導出方法には立ち入りませんので、興味のある方は、参考資料のうち特に「An Explanation of Nakamoto’s Analysis of Double-spend Attacks」を参照してください。

また、確率論の詳しい説明は、サトシが参考文献として挙げている、ウィリアム・フェラー (William Feller) の「An Introduction to Probability Theory and Its Applications, Volume 1 (確率論とその応用)」など、確率論のテキストを参照してください。

余談ですが、フェラーの本は古典的名著と言われています。初版は1950年、最後の第三版は1968年に出ていますが、サトシが参考にしたのは、なぜか1957年の第二版です。筆者はついつい、第二版と格闘する学生時代のサトシを想像してしまいます。

攻撃の成果

第11章は、第6回や第7回で説明したような、誠実なチェーンを追い抜く攻撃について分析しています。

We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain.

ここでは、攻撃者が、誠実なチェーンよりも速く別のチェーンを生成しようとする状況について考える。

実はこの攻撃、成功しても大した成果は得られません。

Even if this is accomplished, it does not throw the system open to arbitrary changes, such as creating value out of thin air or taking money that never belonged to the attacker.

たとえそれが成功しても、無から価値を生み出したり、攻撃者が一度も手にしたことのないお金を取得するなど、システムを勝手に変更できるようにはならない。

コインを偽造したり、強奪したりはできないのです。なぜなら、誠実なノードがブロックやトランザクションを検査し、不正なものは受け入れず、ブロードキャストもしないからです。

An attacker can only try to change one of his own transactions to take back money he recently spent.

攻撃者は、彼が最近使ったお金を取り戻すべく、彼自身のトランザクションを一つ変更しようと試みることしかできない。

攻撃者は、以前所有したことのあるコインを取り戻すこと、つまりは二重使用ぐらいしかできないというわけです。

もっとも、愉快犯であればチェーンを追い抜くこと自体が成果になりうるのですが、以下では、攻撃者は二重使用を目論んでいるものとして読み進めていきましょう。

ランダムウォーク

サトシはまず、攻撃者が誠実なチェーンに追いつく可能性について考えます。

追いつくということは、チェーンの長さが同じになるということです。検討すべきなのは、長さが上回ること、つまり追い抜くことではないかとも思いますが、ここではあまり気にしないことにします。

追いつかれる誠実なチェーンは、もともとは攻撃者より何ブロックかリードしていたはずです。そこから、ある時は誠実なチェーンが１ブロック伸び、またある時は攻撃者のチェーンが１ブロック伸び、ということをくり返して、ついにリードが無くなった時が追いつかれた時なわけです。

このような動きはランダムウォーク (random walk) ※1 と呼ばれ、以下のようなグラフで表すことができます。

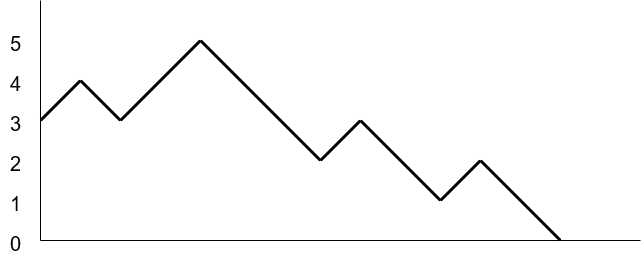
ランダムウォーク

このグラフは、始めに３ブロックあったリードが、増えたり減ったりしてついにゼロとなり、攻撃者に追いつかれてしまったことを表しています。

賭博者の破産問題

こうした動きを、賭けに例えてみましょう。

まず、誠実なチェーンのリードを所持金とみなします。リードが５ブロックであれば、お金を５単位持っていると考えるわけです。

そこから、攻撃者を相手に賭けをします。勝てば誠実なチェーンが１ブロック伸び、負ければ攻撃者のチェーンが１ブロック伸びます。つまり、勝てば所持金が１増え、負ければ１減ります。所持金が０となり破産した時が、リードが無くなった時です。

このような賭けで破産する確率の問題は、賭博者の破産問題 (gambler’s ruin problem) として古くから知られています。サトシは、破産問題に関するフェラー本の第ⅩⅠⅤ章 (3.6) の数式をほぼそっくり持ち出して、追いつかれる確率の式とみなしています。 ※2

賭博者の破産問題の数式

qz の説明が攻撃者視点で書かれていますが、以下では破産する賭博者を誠実なノードとして、この数式の意味を見ていきましょう。

追いつかれる確率

誠実なチェーンが追いつかれる確率は、qz と表します。添え字 z は、最初にリードしているブロックの数です。

p は誠実なチェーンが１ブロック伸びる確率で、q は攻撃者のチェーンが１ブロック伸びる確率です。

追いつかれる確率 qz は、条件によって二つに分かれます。条件となるのが、p と q の大小関係、つまりどちらのチェーンが伸びやすいかです。

条件 p ≤ q のとき、すなわち攻撃者のチェーンの方が伸びやすいか五分五分ならば、qz = 1 です。つまり、いずれ必ず追いつかれます。

条件 p > q のとき、すなわち誠実なチェーンの方が伸びやすいならば、qz = (q/p)z です。条件が p > q ですので、1 > q/p ですね。ということは、z が大きいほど、(q/p)z は小さくなります。つまり、最初のリードが大きいほど追いつかれる確率は小さくなるのです。

これについて、サトシは次のように述べています。

Given our assumption that p > q, the probability drops exponentially as the number of blocks the attacker has to catch up with increases. With the odds against him, if he doesn’t make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind.

p > q の場合、攻撃者が追いつかなくてはならないブロックの数が増えるにしたがい、追いつける確率は急激に下がる。そのように不利な状況で、もしも攻撃者が早い段階でラッキー・ランジをきめられないとしたら、差が開くにしたがい、攻撃が成功する可能性は無視できるほど小さくなる。

ランジというのは、フェンシングで素早く前方に突きを繰り出す技のことです。攻撃者が運よく差をつめられることの例えなわけですが、そうでもしないと p > q の場合、攻撃は成功しそうにないのです。

破産問題による形式化のポイント

この、攻撃を破産問題にあてはめるアイデアについて、筆者が思うポイントを二つ紹介します。

ポイント① ネットワークは分析対象外

明示されていませんが、p と q を決めるのは PoW をこなすパワー、つまり論文で言うところの CPUパワーと考えられます。

例えば、誠実なノードの CPUパワーがネットワーク全体の 60% を占めていれば、攻撃者の CPUパワーは 40% です。つまり p = 0.6, q = 0.4 であり、p > q ですので、誠実なチェーンがリードを十分広げれば、攻撃の心配はほとんどなくなります。

しかし、以下の図のような場合はどうでしょうか。

エクリプス攻撃

左側のボブのグループと、右側のキャロルのグループは誠実なノードです。それぞれ CPUパワーは 30% で、合計 60% です。

両グループの間には、攻撃者アリスのノードが並んでいます。アリスの CPUパワーの合計は 40% であり、誠実なノードの合計を下回っています。

けれどもアリスは、ボブとキャロルの間のブロードキャストを妨害できます。そのため、ボブとキャロルは、それぞれ 30% のパワーで、それぞれ別々のチェーンを伸ばしていくことになります。それに対し、アリスのパワーは 40% ですので、いずれ攻撃は成功してしまうのです。

これは、2015年に米国ボストン大学の Ethan Heilman らが発表したエクリプス攻撃 (eclipse attacks) という攻撃の一パターンです。網目状につながりあう P2Pネットワークに見えても、このように攻撃者によって分断されているかもしれないのです。

破産問題の p, q は、誠実なチェーンと攻撃者のチェーンを単純に二つに分けただけです。また、p, q は一定で変化しません。時々刻々移り変わる、P2Pネットワークの複雑な動きまでは検討していないのです。

ポイント② インセンティブは分析対象外

破産問題の式を示す前に、サトシは以下の仮定を置いています。

Suppose a gambler with unlimited credit starts at a deficit and plays potentially an infinite number of trials to try to reach breakeven.

無限の資金を持つ賭博者が、赤字から始めて収支とんとんになるまで無限回の試行を行う可能性があると仮定する。

要するに、攻撃者は攻撃が成功するまで決してあきらめない可能性があると仮定しているのです。

この仮定は、先ほどの数式の解釈と矛盾するものではありません。フェラー本には、「（qz を）無限の所持金をもつ相手とゲームをした場合の破産の確率と解釈するのに誰もためらわないであろう」と書かれています。「無限の所持金をもつ相手」は、攻撃者に相当します。攻撃者は永遠に破産せず、賭けは誠実なノードが破産するまで続くのです。

現実にはまずありえないこの無限の仮定について、フェラー本の第Ⅰ章１の説明を紹介します。

フェラーは、保険業の実務では人間の寿命に限界を認めていないことを例に、そうした考えは「まったく馬鹿らしくみえるかもしれない」と述べています。けれども、「別に悪いことは起こらないし、たくさんの公式が簡単になるという点で都合がよい」のだそうです。

また、寿命に限界があると認めることは、「x年生きることはできるが、x年と2秒は生きられない」と認めることであり、そうした考えは「寿命にかぎりがないという考えと同じく、魅力のないもの」とも述べています。

それにしても、この第11章の仮定は、第6章「Incentive」と異なるという点でちょっと気になります。第6章の攻撃者は損得を考えて行動していましたが、第11章の攻撃者はまるで別人のように、採算度外視で誠実なチェーンを追い続けるのです。

いつピザを渡すか？

続いてサトシは、より現実的な問題として、ビットコイン・ユーザーの決断について考えます。

We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can’t change the transaction.

ここからは、新たなトランザクションの受信者が、そのトランザクションを送信者が変更できないと十分に確信するまでに、どれだけの時間待たなくてはならないかを考える。

例として、アリスがピザ屋さんからピザを購入する場合を考えてみましょう。アリスは攻撃者で、ピザを手に入れることと、その後でピザの支払に使ったコインを取り戻すことを目論んでいます。

アリスはまず、ピザを手に入れるためコインを支払います。新たなトランザクションを作って、ブロードキャストするのです。このトランザクションは、特に細工のない、ふつうのトランザクションです。

Once the transaction is sent, the dishonest sender starts working in secret on a parallel chain containing an alternate version of his transaction.

トランザクションが送られると、別のバージョンのトランザクションを含む平行なチェーンにおいて、不誠実な送信者は隠れてワークを開始する。

ここでは単純に、攻撃者がチェーンを伸ばし始めるのは、支払を行うトランザクションをブロードキャストした後であると想定しています。冒頭の例のように、攻撃者が神がかった幸運の持ち主で、前もって誠実なチェーンよりはるかに長く自分のチェーンを伸ばしている場合については考えません。 ※3

ピザ屋さんは、いつでもピザを渡すことができますが、ここではしばらくのあいだ待つことにしましょう。破産問題の式が示すとおり、誠実なチェーンが伸びるほど、攻撃が成功する確率は下がるからです。

それでは、いつになったら安心してピザを渡せるのでしょうか。それを考えるには、破産問題の式だけでは足りません。アリスは隠れてチェーンを伸ばしているからです。

He doesn’t know the exact amount of progress the attacker has made

（コインを受け取る）彼は、攻撃者がどれだけ進捗したか正確には分からない

ピザ屋さんは、誠実なチェーンと攻撃者のチェーンとの差が分かりません。もしもアリスが誠実なチェーンを追い抜き、かつピザを手に入れてしまったら、二重使用のトランザクションとブロックをブロードキャストして支払を取り消してしまうでしょう。

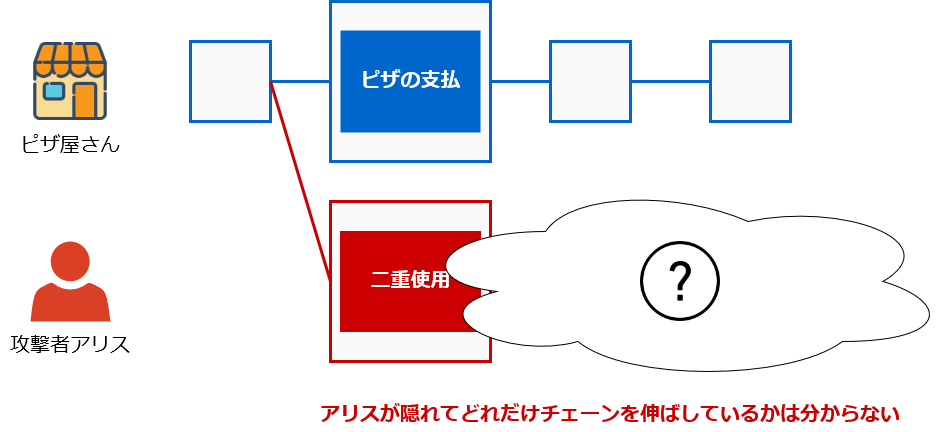
隠れてチェーンを伸ばすアリス

攻撃者は何ブロック伸ばしたか？

例えば、ピザ屋さんが支払を受け取ってから、１００ブロック伸びるまで待ったとしましょう。

その間に、もしも攻撃者アリスが１ブロックしか伸ばせていなければ、リードは９９ブロックです。破産問題の式より、追いつかれる可能性は非常に低いでしょう。

けれども、アリスが９８ブロック伸ばしていたらどうでしょうか？リードはたったの２ブロックです。CPUパワーにもよりますが、追いつかれる可能性がまあまあ出てきます。

また、１００ブロック待つということは、１６時間以上 (１００ブロック x １０分) 待つということです。ピザの注文としてはちょっと待たせすぎです。

それでは２０分、つまり２ブロック待つことにしたらどうでしょうか？ちょっと不安ですね。その間に、アリスが運よくラッキー・ランジをきめて３ブロック伸ばしていたら、攻撃が成功してしまいます。

ピザ屋さんが、絶対確実に安心してピザを渡せるタイミングはありません。けれども、ビットコインを受け取るために、賭けはしなければならないのです。

ポアソン分布

攻撃者が何ブロック伸ばしたかは分からないので、サトシは確率を用いることにしました。

誠実なチェーンが伸びた数を z、その間に攻撃者のチェーンが伸びた数を k とします。すると、追いつかれる確率は以下のようになるはずです。

「誠実なチェーンが z ブロック伸びていたときに追いつかれる確率」
＝「k = 0 になる確率」 x「(z - 0) ブロックの差を追いつかれる確率」
＋「k = 1 になる確率」 x「(z - 1) ブロックの差を追いつかれる確率」
＋「k = 2 になる確率」 x「(z - 2) ブロックの差を追いつかれる確率」
＋ …
＋ …

各行の掛け算の右側、「(z - k) ブロックの差を追いつかれる確率」は、二通りあります。

k ≤ z のとき、すなわちまだ追い抜かれていない場合は、p > q のときの破産問題の式から (q/p)(z - k) となります。p ≤ q のときはというと、いずれ必ず追いつかれるので無視します。ここではピザ屋さんの決断の成否について考えており、どのような決断でも追いつかれる状況を考えても仕方がないのです。

k > z のとき、すなわちすでに追い抜かれていた場合、確率は 1 です。つまり必ず追いつかれます。なぜなら、すでに追い抜かれていたときにピザを渡してしまうと、アリスはすぐに隠していたチェーンをブロードキャストしてしまうからです。

各行の掛け算の左側、k = 0, 1, 2, … それぞれの確率をどうするかは悩みどころです。サトシは、理由を説明せずに、ポアソン分布 (Poisson distribution) をあてはめました。

ポアソン分布は、フェラー本の第Ⅵ章６によると、「一定区間内に、ちょうど k 個の点（事象）が得られる確率」と言えます。誠実なチェーンが伸びている間に、攻撃者のブロックが k 個伸びた確率として使えそうです。

ポアソン分布を用いると、追いつかれる確率は以下のようになります。

ポアソン分布を用いた計算

実は、このアイデアに対しては、後にいくつか反論が出されています。ポアソン分布ではなく負の二項分布を使用する方がよいだとか、ポアソン分布のせいで理論値とシミュレーション結果とがずれるだとかいうものです。しかし、以下ではサトシにしたがい、ポアソン分布を用いて追いつかれる確率を計算してみましょう。

追いつかれる確率：攻撃者が伸ばしたブロック数が分からない場合

計算は、Ｃ言語のプログラムで行います。上記の式は k に上限が無く、計算が終わらないので、次のように変形します。

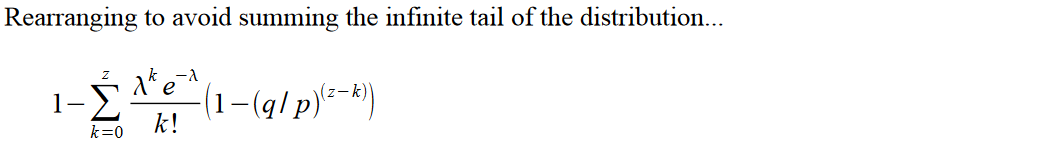
ポアソン分布を用いた計算２

論文には、この式を実装した関数が載っています。

関数 AttackerSuccessProbability

具体的な確率を計算するには、まず q を決める必要があります。q は攻撃者のチェーンが１ブロック伸びる確率でしたね。 p + q = 1 ですので、q が決まれば p は自動的に決まります。

q を決めたら、z の値をいろいろ変えて、確率がどうなるか試します。論文には、以下のように q = 0.1 と 0.3 の例が示されています。

q = 0.1 と 0.3 の例

z が増えるにつれて、追いつかれる確率 P が急激に下がっていますね。

参考までに、上記の結果を出力するコードを書いてみましたので自由にご利用ください。

#include <stdio.h>
#include <math.h>

double AttackerSuccessProbability(double q, int z)
{
    double p = 1.0 - q;
    double lambda = z * (q / p);
    double sum = 1.0;
    int i, k;
    for (k = 0; k <= z; k++)
    {
        double poisson = exp(-lambda);
        for (i = 1; i <= k; i++)
            poisson *= lambda / i;
        sum -= poisson * (1 - pow(q / p, z - k));
    }
    return sum;
}

void PrintProbabilities(double q, int z[], int len)
{
    double P;
    int i;

    printf("q=%.1f\n", q);
    for (i = 0; i < len; i++)
    {
        P = AttackerSuccessProbability(q, z[i]);
        printf("z=%-5iP=%.7f\n", z[i], P);
    }
}

int main()
{
    int z1[11] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    PrintProbabilities(0.1, z1, 11);

    printf("\n");

    int z2[11] = {0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50};
    PrintProbabilities(0.3, z2, 11);

    return 0;
}

６ブロック待つ慣習

さらにサトシは、q もいろいろ変えて試し、追いつかれる確率 P が 0.1% になる場合を列挙しています。

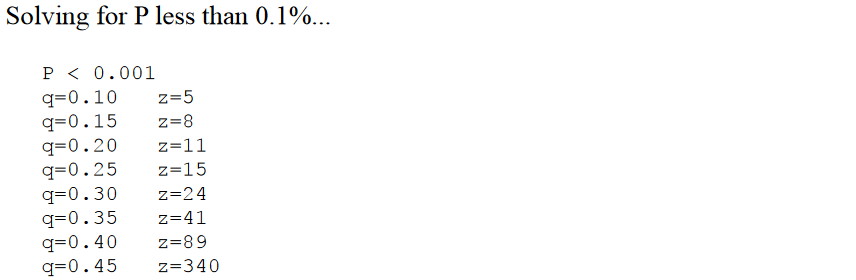
追いつかれる確率が 0.1% を下回る例

慣習として、ビットコインは支払が確定するまで６ブロック待てとよく言われます。上記の結果で近いのは、q = 0.10 の場合ですね。攻撃者の CPUパワーが 10% の時は、z = 5 ブロック待てば千に一つも追いつかれないので、まあ大丈夫だろうというわけです。

ただし、慣習にしたがったからといって、支払が完全に確定するわけではありません。サトシが仮定したように、攻撃者はずっと誠実なチェーンを追い続けているかもしれません。

もしもいつか攻撃が成功し、コインを取り戻されたとしても、銀行やクレジットカード会社など、助けてくれる TTP はいません。

ビットコインのユーザーは、サトシが示してくれた数式を参考に、サトシが分析しなかったネットワークやインセンティブなども適宜考慮しながら、自分自身で決断し、賭けなければならないのです。

おわりに

今回は、第11章「Calculations」で分析されている、二重使用攻撃の確率について見てきました。

残る第12章「Conclusion」はまとめであり、本論としてはこの第11章が最後でした。この連載も、今回でひとまず終了です。

当初の構想としては2、3回で完結させるつもりが、思いがけず全11回、1年にわたる連載となりました。第1回で書いたように、読者の皆様にとって少しでもブロックチェーンについて考える「ヒント」になれたならば幸いです。それでは、良いお年をお迎えください。

注

※1: 論文では「二項ランダムウォーク (Binomial Random Walk)」と呼ばれていますが、フェラー本では「一次元ランダムウォーク (one-dimensional random walk)」または単にランダムウォークと呼ばれています。

※2: フェラー本では、「古典的な破産の問題 (the classical ruin problem)」として、賭博者 (誠実なノード) と相手 (攻撃者) の所持金の合計を a とし、賭博者の所持金がゼロ (誠実なノードが破産) または a (攻撃者が破産) のどちらかになるという状況を考えています。その a を無限大としたのが、ビットコイン論文で用いられている式です。破産問題の起源はホイヘンスやフェルマー、パスカルまでたどれるそうですが、詳しくは参考資料の「確率は迷う」を参照してください。

※3: 以下のように、論文には、前もってチェーンを準備することは防げるという趣旨の記述があります。

The receiver generates a new key pair and gives the public key to the sender shortly before signing. This prevents the sender from preparing a chain of blocks ahead of time by working on it continuously until he is lucky enough to get far enough ahead, then executing the transaction at that moment.

(コインの) 受取人は、署名する少し前に、新たな鍵ペアを生成して公開鍵を支払人に渡す。そうすることで、支払人がチェーンをずっと先まで伸ばせる幸運が訪れるまでワークをし続け、前もってブロックのチェーンが準備できてから取引を行うことを防ぐことができる。

しかし以下のように、この記述については疑問符がつけられています。

参考資料