今回はビットコイン論文の第4章「Proof-of-Work」を読みながら、PoW について見ていきます。ビットコインの PoW はもちろん、元祖 PoW と言えるドワーク&ナオアの提案や、実際に手を動かして PoW を体験する方法も紹介します。
前回のおさらい
前回見たとおり、サトシは二重使用問題を解決するために、タイムスタンプ技術を取り入れることにしました。しかし、参考にした TIMESEC など従来の方式は、信頼できる第三者すなわち TTP に基づいていました。
サトシは TTP を必要としない分散タイムスタンプサーバーを作ろうと考えます。そのために、新聞のかわりに導入したのがプルーフ・オブ・ワーク (proof-of-work) 略して PoW のシステムです。
「PoW」という用語
PoW という用語は、ビットコインによって一躍有名になりましたが、そもそもは1999年の論文 (extended abstract)「Proofs of Work and Bread Pudding Protocols」で作り出された言葉と言われています。
その論文は、当時あったいくつかの研究 ※1 の共通点を整理し、PoW の形式的な定義を試みているのですが、おおまかに言うと PoW とは「ある水準のワークをある特定の時間をかけて行ったことを明らかにするプロトコル (This is a protocol in which a prover demonstrates to a verifier that she has expended a certain level of computational effort in a specified interval of time.)」なのだそうです。
ここでいうワークは、もちろん人間が行うのではなく、コンピューターが行う計算処理のことです。プロトコルというのは、決まりごとや手順のことですね。PoW とは、コンピューターがそれなりの時間きちんと働いたことを証明する方法を定めたものだというわけです。
ハッシュキャッシュの PoW
さまざまな PoW がある中で、サトシはハッシュキャッシュ (Hashcash) にならった PoW システムを作ることにしました。
ハッシュキャッシュの考案者アダム・バック (Adam Back) は、まず1997年に実装を公開し、その後改良を重ね整理した理論を2002年に論文として発表しています。
ハッシュキャッシュの PoW については、ビットコイン論文の第4章「Proof-of-Work」でごく簡単に説明されています。
The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits.
そのプルーフ・オブ・ワークでは、ある値をつぶさに調べて探し当てることになる。その値とは、例えば SHA-256 を用いて、ハッシュ化すると先頭の数ビットがゼロとなる値である。
SHA-256 の「SHA」とは、「Secure Hash Algorithm」の略です。その名のとおり、SHA-256 はハッシュを算出するためのアルゴリズムを規定したもので、ハッシュアルゴリズムやハッシュ関数 (hash function) と呼ばれます。
ハッシュキャッシュが採用したのは SHA-1 という別のハッシュ関数でしたが、ビットコイン論文の発表当時、SHA-1 は安全性が懸念されるようになっていました。そのため、かわりに次世代のハッシュ関数 SHA-2 の一つである SHA-256 に差し替えられたのでしょう。
前回も説明したとおり、データをハッシュ化すると「CE714BACCF60B190E7978BF56E31737C」のような意味不明で不規則な値になります。これが「00000000CF60B190E7978BF56E31737C」のように、先頭の何桁かがゼロになるようなデータを探すのが PoW だというわけです。
「bits」と書かれているので、「00101101…」のような 0 と 1 のビット列が想定されていることになりますが、本記事では16種類の文字 (0 ~ 9 と a ~ f) による16進表記で説明していきます。
くじ引きとしての PoW
不規則と言っても、SHA-256 を用いれば、同じデータからはいつも同じハッシュが算出されます。けれども、どんなデータからどんなハッシュが出てくるかは、やってみないと分かりません。やってみないと分からないので、ただひたすら、ハッシュの計算という地道なワークをこなしていかなければならないのです。
こうした処理は「パズル (puzzle)」と表現されることがありますが、ジグソーパズルやクロスワードパズルのように、推理力や雑学が役に立つわけではありません。
むしろ、よく言われるように「くじ引き (lottery)」や「抽選」の方が近いように思われます。アタリかハズレか引いてみないと分からないくじを、アタリが出るまで素早く何回も引き続けるようなものだからです。
さわって理解する PoW 入門
ではここで、そのくじ引きのようなワークを体験してみましょう。
そのためには、SHA-256 を計算できなくてはなりませんね。ネットには、ハッシュを計算してくれるサービスがたくさんありますので、その中から今回は DuckDuckGo を利用することにしましょう。
DuckDuckGo は検索サービスの一種ですが、「Instant Answer」という機能により、検索と同じ操作でハッシュを計算することができます。さっそく https://duckduckgo.com/ を開いて、「sha256 Block1Nonce1」と検索してみましょう。
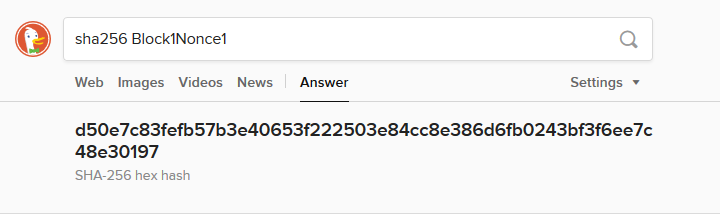
「d50e7c83fe…」と表示されていますね。これが「Block1Nonce1」という文字列の SHA-256 ハッシュです。
ハッシュの先頭2文字は「d5」で、ゼロではありませんね。この先頭2文字がゼロになることを目標に、データを探していきましょう。
「Block1Nonce1」のハッシュは何度計算しても変わりませんので、末尾の数字を一つ増やして「Block1Nonce2」としてみます。
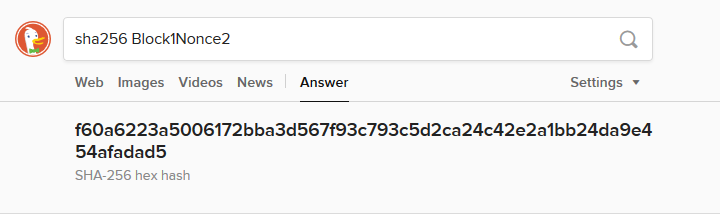
やはりゼロになりませんね。しかたないので、次は「Block1Nonce3」、それがだめなら「Block1Nonce4」という風に、少しづつデータを変えて試していかなければなりません。
これは非常に手間ですし、やりすぎて DuckDuckGo に負荷をかけるのは避けたいので、適当なところでストップしてください。
以下は、筆者が手元で計算した結果です。
| データ (文字列) | ハッシュ (SHA-256) |
|---|---|
| Block1Nonce1 | d50e7c83fefb57b3e40653f222503e84cc8e386d6fb0243bf3f6ee7c48e30197 |
| Block1Nonce2 | f60a6223a5006172bba3d567f93c793c5d2ca24c42e2a1bb24da9e454afadad5 |
| … | … |
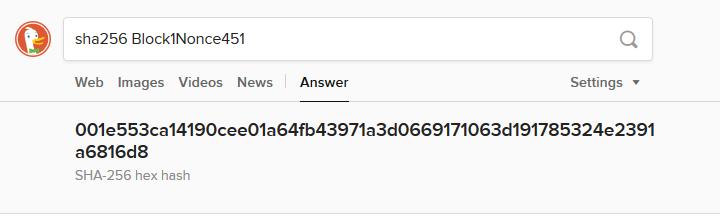
| Block1Nonce451 | 001e553ca14190cee01a64fb43971a3d0669171063d191785324e2391a6816d8 |
| … | … |
| Block1Nonce4379 | 0000B9265692656EF354C37CD47C082012EBE020CEE6B48B246FB3E38E667C64 |
計算を451回繰り返して、ようやく一つ、先頭2文字がゼロになるデータが見つかりました。
目標を一つ上げて、先頭3文字がゼロになるハッシュを探したところ、表のとおり4379回目で見つかりました。たまたまですが、4文字目もゼロになっています。
ところで、これらのハッシュは本当に正しいのでしょうか?それを確かめるには、次のようにたった1回ハッシュを計算するだけでよいですね。
PoW の難易度と検証
こうした PoW の特徴について、サトシは次のように述べています。
The average work required is exponential in the number of zero bits required and can be verified by executing a single hash.
必要とされる平均的なワークは、必要とされるゼロの数に応じて急激に増えるが、検証は一つのハッシュを計算すればよい。
運が良ければ、たまたま1回目に選んだデータで、たまたま目標を達成できることもあるでしょう。
けれども、そんなことは滅多にありません。ふつうは、目標となるゼロの数を増やすにしたがい、ワークの量もどんどん増えていきます。逆にゼロの数を減らせば、ワークの量は減ります。これは、目標となるゼロの数を変えることで PoW のタイヘンさ、つまり難易度 (difficulty) を調整できるということでもあります。※2
一方で、ワークの検証は、難易度にかかわらずたった一つのハッシュを計算するだけで済みます。
このように PoW とは、実行するのはタイヘンで検証するのはラクなものなのです。
ビットコインの PoW
それでは、ビットコインはどのように PoW を行うのでしょうか。第4章の続きを読んでみましょう。
For our timestamp network, we implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block’s hash the required zero bits.
本論文のタイムスタンプ・ネットワークでは、プルーフ・オブ・ワークを行うにあたり、ブロックのナンスを増やしていく。ブロックのハッシュに、必要な数だけゼロが出てくるまで、ナンスを増やしていくのである。
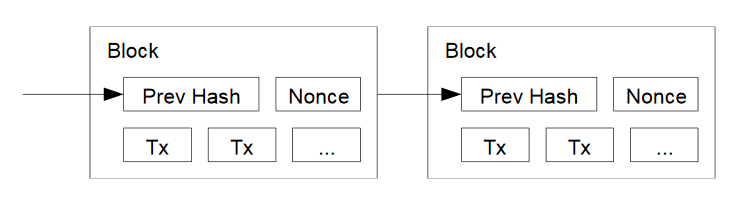
言い回しは違いますが、基本的なアイデアはハッシュキャッシュと同じです。ブロックをハッシュ化して、先頭の何桁かがゼロになるようにするのです。
ブロックには、トランザクションなどの他に、ナンス (nonce, ノンス) という数値を含めます。先ほどの PoW 入門では、文字列の末尾の数字を 1, 2, 3 … と増やしていきましたね。同じように、ビットコインの PoW では、ブロックのナンスを 1, 2, 3 … と増やしながらハッシュを計算していきます。
ナンスという用語はビットコインに限らない、セキュリティ技術の用語です。そもそもは何百年も前からある言葉で、「当座」や「臨時」という意味が示すとおり、ナンスはつど使い捨てにされます。
図の「Prev Hash」は、一つ前のブロックのハッシュです。「Prev Hash」をブロックに含めることで、前回見たリンキングを行っているわけです。
Once the CPU effort has been expended to make it satisfy the proof-of-work, the block cannot be changed without redoing the work.
ひとたび CPU の働きがプルーフ・オブ・ワークを成し遂げるために費やされたら、そのワークをやり直すことなしにブロックを変更することはできない。
ブロックの中身が変わればハッシュも変わるので、ワークもやり直しになります。
As later blocks are chained after it, the work to change the block would include redoing all the blocks after it.
ブロックの後ろにはブロックがつなげられていくので、ブロックを変更するワークには、その後ろの全てのブロックのワークをやり直すことが含まれることとなる。
リンキングの特徴そのままですね。ブロックのチェーンを伸ばしていくと、その分だけやり直しに必要なワークも増えていきます。
もしもワークをさぼって不正なリンキングを行ったところで、検証は簡単ですので、誰かが検証すればたちまちばれてしまいます。検証する人がいる限り、地道にワークを行うしかないのです。
競争としての PoW
このような PoW を「タイムスタンプ・ネットワーク」で行う、と書かれていることに注意しましょう。ビットコインの PoW では、ネットワークに散らばる複数の分散タイムスタンプサーバー、すなわちノード (node) が、それぞれ一斉にワークを行うのです。
次回以降もう少し詳しく見ていきますが、基本的に、どれか一つのノードが目標のハッシュを見つけたら、PoW 1回分は終了です。そのハッシュでブロックはリンキングされ、また次のブロックに対する新たな PoW が始まります。このため、ビットコインの PoW は、どのノードが一番早く目標のハッシュを見つけられるかの競争 (race) ととらえることができます。
競争を有利に進めるには、ハッシュの計算速度を上げるとよいですね。先ほどは PoW をくじ引きにたとえましたが、くじは何度でも引けるので、なるべく素早く何回も引く方がアタリも出やすいのです。
それならば一番計算の速いノードが必ず勝つかというと、そうでもありません。
実は、ブロックにどのトランザクションを含めるか、つまりどのトランザクションにタイムスタンプを発行するかは、各ノードが自由に決められます。また、ブロックには通常各ノード固有の情報などが含まれます。意図的にそれらを一致させようとしない限り、各ノードがハッシュ化するブロックはそれぞれ違うものになるのです。
ブロックが異なれば、ハッシュの出方も異なり、アタリを引くまでの時間も異なってきます。この競争は、スピードだけでなく、運の要素も絡んでくるわけです。
元祖 PoW
ところで、今でこそ PoW の代表例といえばビットコインとなりましたが、PoW のルーツをたどってみると、また違った姿が見えてきます。
冒頭の「PoW」という用語を作った論文によると、元祖 PoW と言えそうなのは、1993年の論文「Pricing via Processing or Combatting Junk Mail」です。
論文の著者、シンシア・ドワーク (Cynthia Dwork) とモニ・ナオア (Moni Naor) によると、その元祖 PoW を考えた一番の動機は、迷惑メール (junk mail) に対抗することだったそうです。
迷惑メール対策の検討
電子メールは簡単かつ低コストで大量に送信できる。この特徴は、ほとんど悪用を招いているも同然である。そう考えたドワーク&ナオアは、以下の二つの対策を検討します。
一つ目は、悪用を禁止する法律 (legislation) を制定することです。迷惑メールを犯罪とみなすのですね。けれども、なにが迷惑メールでなにが普通のメールかを定義するのは、ちょっと考えただけでも難しそうです ※3 。ドワーク&ナオアは計算機科学者ですし、この対策は検討対象から外します。
もう一つは、メールを送るごとにシステムの利用料 (usage fees) をとることです。郵便物に切手を貼るように、メール一通ごとにお金を払ってもらうのですね。あいかわらず迷惑メールは送れますが、コストがかさむ分、抑止 (deterrent) することはできるでしょう。
けれども、これではなんだか電子メールの利点が損なわれている気がします。重たい郵便物に高い切手を貼るように、データサイズの大きなメールにはより高額の利用料を請求するのでしょうか。
プライシング関数とショートカット
ドワーク&ナオアは、単なる利用料とは異なる種類のコストを課そうと考えます。その中心となるアイデアがプライシング関数 (pricing function) とショートカット (shortcut) です。
アイデア① プライシング関数
プライシング関数は、ワークを定義した関数です。定義を行うのは、プライシング局 (pricing authority) といういわば TTP で、全てのユーザーはその定義に従わなくてはなりません。
プライシング局は、ワークの難易度を、易しい (easy) のでもなく、難しい (hard) のでもなく、ほどよい (moderate) ものに調整します。易しすぎると意味が無いですし、難しすぎてなかなか終わらないのも都合が悪いからです。
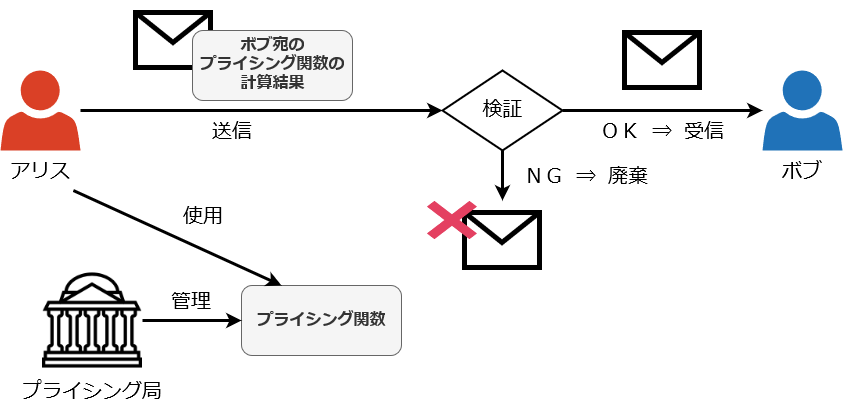
図のように、アリスはプライシング関数でワークを行い、その計算結果をメールとともに送ります。計算結果は途中で検証され、OK ならボブはメールを受信できるようになります。NG ならメールは廃棄され、ボブはメールが送られてきたことに気付きません。
プライシング関数はほどよい難易度なので、一通のメールを送るだけなら特に問題になりません。けれども大量のメールを送ろうとすると、ほどよい難易度がつもりつもって重い負担となります。迷惑メールを大量に送ることが、難しくなるわけです。
アイデア② ショートカット
ただ、これでは迷惑メールだけでなく、普通のメールを大量に送ることも難しくなります。たとえば、イベント参加の当選・落選通知を大勢の応募者に送るような場合です。そのような場合は、ショートカットを使えるエージェントに手数料を払います。
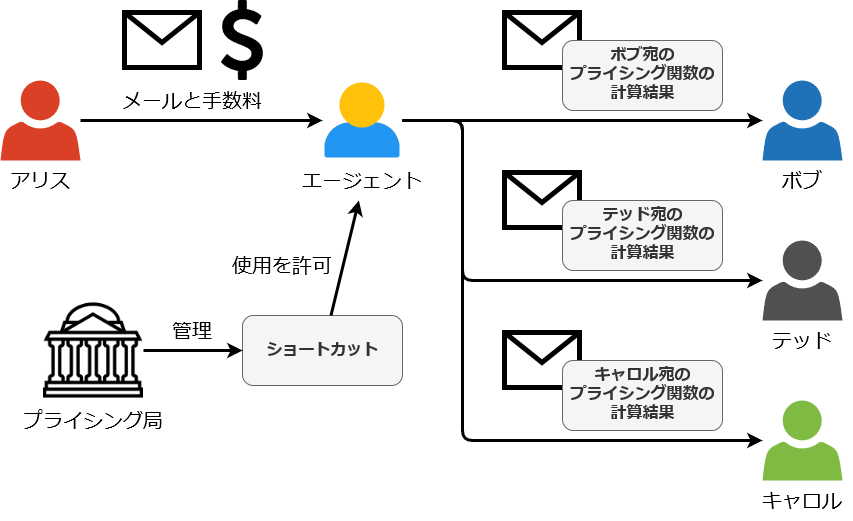
ショートカットは、プライシング関数を手間をかけずに処理できるようにする「近道」です。別名トラップドア (trapdoor) ※4 とも呼ばれるように、普段はプライシング局が非公開で管理しています。
図のエージェントは、信頼できるエージェント (trusted agent) であり、プライシング局からショートカットを教えてもらえる立場にあります。そのため、アリスにかわってプライシング関数を易々と処理し、大量のメールを送ることができるというわけです。
PoW はもったいない?
ドワーク&ナオアのシステムは、利便性をあまり損なわずに迷惑メールを抑止することを目指したものと言えるでしょう。そのために、プライシング局という TTP を導入し、プライシング関数をほどよい難易度に保つとともに、必要とあらばショートカットの利用を許可するわけです。
さらに彼らは、今後の課題として、プライシング関数で役に立つ処理を行うことを挙げています。今のところ、プライシング関数は迷惑メールを抑止しているだけで、それ以外には役に立つことをしていない (no useful purpose) と言うのです。
たしかに、論文には三種類のプライシング関数が提案されているのですが、いずれもたくさん計算が必要だとか、時間がかかるというだけです。例えば、どこかの企業の会計処理をしてくれるとか、建築物の構造計算をしてくれるとか、現実の仕事を処理するために行われる計算ではないのです。
残念ながら、彼らは具体的にどんな役に立つ処理をさせるかまでは提案していません。また、迷惑メールを抑止できれば十分だという考え方もあるかもしれません。けれども、PoW はそのはじまりにおいて、言わば「もったいない」という問題意識があったということは、おぼえておいてよいでしょう。
難易度の基準
プライシング局の無いビットコインでは、あらかじめ決められた基準にしたがって、PoW の難易度を調整します ※5 。論文には書かれていませんが、その基準とは、平均して1時間に6ブロック、つまり10分間に1ブロック生成することです。
10分という時間の「ほどよさ」について、サトシは厳密で精緻な理論を展開しているわけではありません。9分や11分にすると大きな問題が生じるなどとは、考えていなかったでしょう。ただ、ワークがあまりに短時間で終わると、まとめてタイムスタンプを発行するラウンド方式にした効果が薄れてしまいます。逆にあまりに長時間ためこんでから発行していては、支払システムとしては不便でしょう。
ショートカットはありません。あくまで基準に沿って調整された難易度にしたがい、ワークを行う必要があります。
難易度の調整は、2016ブロック生成されるごとに行うことになっています。2016ブロックということは、約2週間ということです。(1ブロック10分 ⇒ 6ブロック1時間 ⇒ 144ブロック24時間 ⇒ 2016ブロック14日)
調整はそれぞれのノードが自主的に行います。ズルをしないよう検証する必要がありますが、そうした仕組みは次回以降に見ていきます。
難易度の調整
難易度の調整については、第4章の最後に説明されています。
To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour.
ハードウェアの速度の上昇やノードを稼働させることへの関心の変化を時とともに相殺するため、1時間当たりのブロックの平均的な数に関する移動平均によって、プルーフ・オブ・ワークの難易度は決定される。
ブロックが生成される速さは、時とともに変化し、1時間当たり6ブロックという基準からズレていきます。そのズレを、PoW の難易度を調整することで帳消しにすると言っています。
ブロックが生成される速さは、ワークを行う複数のノードを合わせた、全体的な処理能力により変化します。
例えば、ノードが最新の高速なハードウェアに買い替えたり、ビットコインが注目を集めてノードが増えたりすれば、全体として短時間でより多くのワークをこなせるようになり、ブロックが生成される間隔も短くなっていくというわけです。
PoW のコスト
難易度の調整は、TTP なしに PoW のシステムを運用するという点では有効と言えそうです。
しかし、コストという観点ではどうでしょうか。
If they’re generated too fast, the difficulty increases.
もしそれら(ブロック)が非常に速く生成されるならば、難易度は増大する。
これはつまり、ハードの性能を上げたり台数を増やしたりして、コストをどれだけかけたとしても、平均10分間に1ブロック生成されることに変わりはないということです。一時的にはブロックの生成間隔は短くなるでしょう。けれども、おおよそ2週間たてば難易度は調整され、元に戻るのです。
得られる成果がブロックだけだと考えるならば、同じ成果を得るためにより多くのコストをかけていることになります。成果が同じならコストはなるべくかけない方がよいのではないでしょうか。
ところが、ビットコイン論文には、PoW のコストについて論じている箇所はありません。
第2回で見たとおり、ビットコイン論文は現行システムの弱点をコストの観点から論じています。それにもかかわらず、そもそもコストをかけさせる技術である PoW については、問題ないとも、もったいないとも書いていないのは、驚くべきことと言えるでしょう。
PoW とコンセンサスアルゴリズム
論文とは異なり、ビットコインの PoW のコストについては盛んに議論されています。特に電力消費については、批判的な記事を目にしたことがある方も多いでしょう。PoW のかわりに、より効率的で優れた仕組みを採用したと謳うブロックチェーン・プロジェクトもいくつもあります。
それらさまざまな意見やブロックチェーン・プロジェクトを評価・検討するためには、コストとともに、そのコストを支払って実現されることはなんなのかもきちんと理解する必要があるでしょう。
第3回で見たとおり、サトシは TTP を用いずに二重使用対策を行うため、各ノードがトランザクションのたったひとつの順番に合意できるような仕組みが必要と考えました。
ブロックチェーンの世界では、「PoW はコンセンサスアルゴリズム (consensus algorithm, 合意形成アルゴリズム) の一種である」とよく言われます。しかし、今回見たとおり、PoW はブロックを生成する速さを一定に保つものであり、それだけで合意に至るものではありません。PoW は、コンセンサスアルゴリズムで用いられる技術要素、と言った方がより適切でしょう。ビットコインの合意形成の仕組みを「ナカモト・コンセンサス (Nakamoto Consensus)」と呼んで、PoW と明確に区別することもあります。
サトシは PoW を用いて、どのように合意が実現されると言っているのか、その説明はまた次回としたいと思います。
おわりに
今回はビットコイン論文の第4章「Proof-of-Work」を読みながら、PoW について説明しました。
PoW は、実行するのはタイヘンで、検証するのはラクなものです。「さわって理解する PoW 入門」と題して、その特徴を体験する方法も紹介しました。
PoW にはさまざまな種類が存在します。元祖 PoW と言えるドワーク&ナオアの迷惑メール対策は、プライシング局という TTP にプライシング関数とショートカットを管理させ、利便性をなるべく損なわないようにしたシステムでした。
ビットコインの PoW は、アダム・バックのハッシュキャッシュを参考にしています。あらかじめ決めておいた基準に沿って難易度の調整が行われますが、そのコストについては論文中ではふれられていません。
PoW や、その代替技術を用いたブロックチェーン・プロジェクトを評価・検討するには、そのコストとともに、何が実現されるのかもきちんと理解する必要があります。PoW は、二重使用対策に必要とされる合意形成の仕組みで利用されます。合意形成の仕組みがどのようなものかは、次回以降見ていきます。
注
※1: 当時すでに公開されていたハッシュキャッシュにはふれられていません。
※2: ソースコード上は、ある数 (例えば 00111010) 以下になることを目標にワークを行っており、先頭のゼロの数だけで難易度が決まるわけではありませんが、本記事ではビットコイン論文の記述に沿って説明します。
※3: 例えば、論文の数年後に発生した「Spam King」ことサンフォード・ウォーレス (Sanford Wallace) の事例を参照
※4: 罠とか落とし穴の類ではなく、この場合は「床板のように見える扉を開くとそこには秘密の地下室があった!」という類のものです。
※5: サトシによると、難易度の調整がはじめて行われたのはリリースから約1年後の2009年12月30日だったそうです。
参考資料
- Adam Back. Hashcash の実装を公開した時のメール, 1997
- Adam Back. Hashcash - A Denial of Service Counter-Measure, 2002
- Cynthia Dwork, Moni Naor. Pricing via Processing or Combatting Junk Mail, Advances in Cryptology - CRYPTO’ 92, 1993
- Markus Jakobsson, Ari Juels. Proofs of Work and Bread Pudding Protocols (Extended Abstract), Springer, Boston, MA, 1999 ※スライド有
- Ari Juels, John Brainard. Client Puzzles: A Cryptographic Countermeasure Against Connection Depletion Attacks, NDSS Symposium, 1999
- Ronald L. Rivest, Adi Shamir. PayWord and MicroMint (extended abstract), 1996 ※スライド有
- Fabian Monrose, Peter Wyckoff, Aviel D. Rubin. Distributed Execution with Remote Audit, In Proceedings of the ISOC NDSS Symposium, San Diego, 1999
- FIPS 180-1 (SHA-1), NIST, 1995
- FIPS 180-2 (SHA-2: SHA-256 等), NIST, 2002
- FIPS 180-4 (SHA-1, SHA-2 最新), NIST, 2015
- Arvind Narayanan 他. Bitcoin and Cryptocurrency Technologies, Princeton University Press, 2016 ※ 特に 5.3.「ENERGY CONSUMPTION AND ECOLOGY」
- ビットコインとエネルギー消費、発熱に関する議論(サトシの投稿有), Bitcoin Forum, 2010
