「<オージス総研をとりまく>人工知能技術の過去と現在（上）」

１．はじめに

　平成29年度4月より10月まで「＜オージス総研をとりまく＞人工知能技術の過去と現在」を連載してまいりました。年度末である今月と来月は、内容をふり返るとともに、年代順ではなく主にキーワードを中心に解説したいと思います。（年代順は下記参照）
２．人工知能技術の変遷　

２．ニューラルネットワーク、ディープラーニング

　まず、人工知能の中心的存在である（ディープラーニングを含む）ニューラルネットワークについて説明します。

２－１．ニューラルネットワーク（Back Propagation）

（１）1980年代後半を通してニューラルネットワーク（Back Propagation）がブームとなった。ニューラルネットワークは中間層（隠れ層）が多い場合、Back Propagationが前まで伝わらないという欠点もあり、中間層は1層～2層が中心であった。第2次ＡＩブーム後もデータ解析（機械学習）の一手法などで使い続けられることになる。
（２）図１の重み付け（W１、W２）がすべての訓練データに対して誤差が最小になるように調整する。基本的には、2乗誤差の合計を最小にする。（Back Propagationの詳細は、以下を参照）

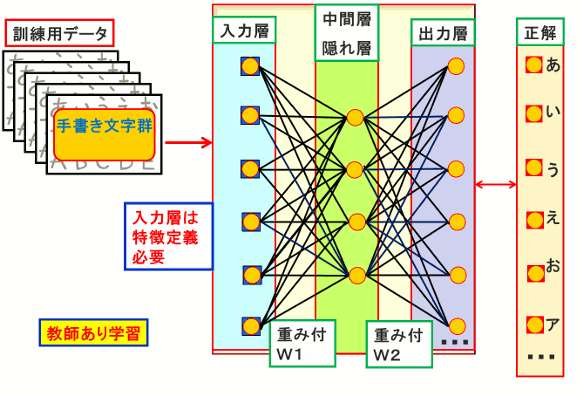
図１．Back Propagation

２－２．「教師なし学習」ディープラーニング

（１）2000年代に入り、まず、入力層と出力層に同じデータを対応させるAuto Encoderを多段階にした「教師なし学習」によるディープラーニングが有名になった。
（詳細は以下を参照）
「<オージス総研をとりまく>人工知能技術の過去と現在（５）」

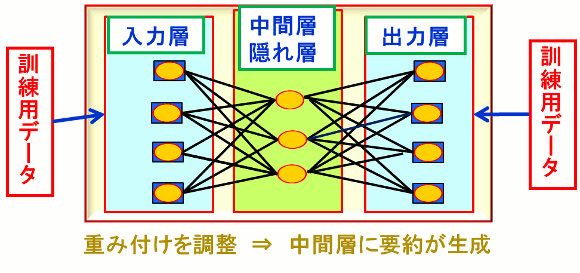
図２．Auto Encoder

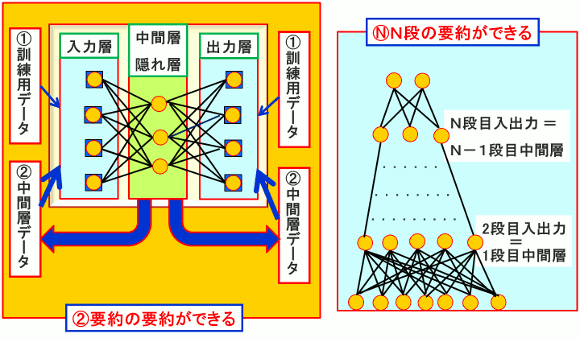
図３．Auto Encoder型ディープラーニング
（松尾豊著「人工知能は人間を超えるか」Ｐ161参考）

２－３．「教師あり学習」ディープラーニング

（１）その後「教師あり学習」が主流になっている。その代表格が、1979年大阪大学福島邦彦教授が提案したネオコグニトロンを原型とするＣＮＮ (Convolutional Neural Network) である。
（２）CNNは、画像データが利用しやすいようにConvolution（畳み込み演算）によるフィルタ（Smoothing、ノイズ除去、エッジ検出などの）機能が含まれている。
（３）各ノードの出力に用いられる活性化関数に、Rectified Linear Unitsを採用したのも、Back Propagationによる多層のディープラーニングが可能になった一因である。
（４）Grad-CAMという技術を使うと、画像のどの箇所を見て判断したかをヒートマップでわかる。
（５）３ＤＣＮＮ（２Ｄ空間＋１Ｄ時間）を使えば、３ＤでConvolutionを行うので、動画を対象にすることができる。
（詳細は以下を参照）
２．ＣＮＮ (Convolutional Neural Network)

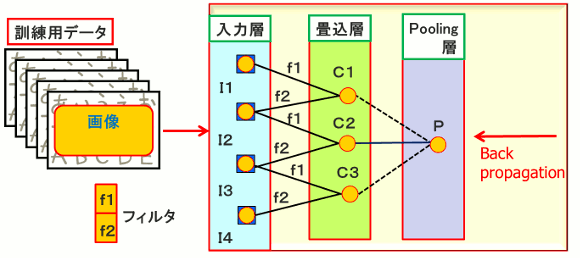
図４．簡単化したＣＮＮ(Convolutional Neural Network)

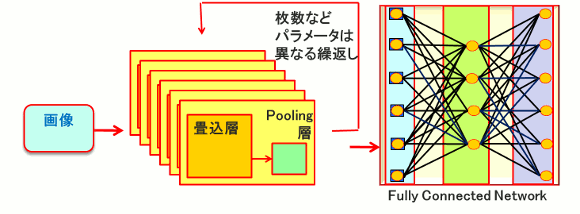
図５．一般化したＣＮＮ

図６．Grad-CAMによるＣＮＮの注目箇所
（Citation from Reference 1. Fig. 1）

３．探索、最適化

３－１．数理計画法

数理計画法などの最適化手法はかつて人工知能に含まれ、エキスパートシステムが経験的解法に対して論理的解法と呼ばれていました。
（１）ある「制約条件」のもとで「評価関数」の最小値または最大値を求める。
（２）制約には「ハード制約」と「ソフト制約」がある。ハード制約は、条件を満たさないと解にはならない。ソフト制約は優先順位。
（３）通常は非線形の式を解く。すべて解くと図７のように、どこが最大値かわかるが、最初はまったくわからない（山に霧がかかった状態）解く方法には「メタヒューリスティック法」などがある。場合によっては極大値を結論としてもよい。
（４）「メタヒューリスティック法」には、山登り法などがあるが、広い意味ではBack PropagationやGenetic Algorithmも含まれる。
（数理計画法は、以下も参照）
「ビジネスを解析する手法とその比較（上）」

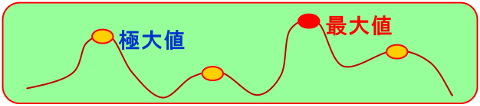
図７．非線形問題

３－２．組合せ最適化

（１）選べる組合せの中から最適なものを選択する。一般的に、ほとんどの最適化問題が範疇に入ると考えられる。数理計画法もそうである。
（２）学生時代に知能ロボットの研究の際、障害物回避を含め最短時間経路探索するのにダイナミックプログラミングで最短経路を決定した。（詳細は以下を参照のこと）
３．大学院時代の研究内容　

３－３．ゲームの理論

（１）ゲームの先読みにおいて数手先の状況について、評価関数を使って正しく判断することが必要である。自分の手が最大値になり、相手も最大値（自分にとっては、最悪値）の手を打つと仮定して、自分の手を決める。この手法をMiniMaxと呼んでいる。
（２）コンピュータハードとコンピュータ科学の発展に伴い、強力なゲームソフトが出現するようになった。その一つがアルファ碁である。
（３）アルファ碁の戦略は非常に複雑なようなであるが、次のように単純化すれば理解しやすい。
(A)序盤：「（強い棋士の16万局を使ったＣＮＮによる）次の各手の確率」を主に使用
(B)中盤：「（3000万データで強化学習した）局面での勝率予測値」を主に使用
(C)終盤：「モンテカルロ木探索」を主に使用
（４）昨年10月アルファ碁ゼロが発表された。これは教師なしの強化学習だけで、アルファ碁を圧倒した。現実の世界への応用の可能性がある。
（詳細は以下を参照）
「<オージス総研をとりまく>人工知能技術の過去と現在（７）」

※続きは次号で述べます。

「Reference」

1. Ramprasaath R. Selvaraju， Michael Cogswell ， et al，: "Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization"， Mar 2017

*本Webマガジンの内容は執筆者個人の見解に基づいており、株式会社オージス総研およびさくら情報システム株式会社、株式会社宇部情報システムのいずれの見解を示すものでもありません。

• 「行動観察とIT～前篇：顧客意図を把握するということ～」 前の記事へ
• 「サービスデザイン思考の現場感」 次の記事へ

『WEBマガジン』に関しては下記よりお気軽にお問い合わせください。

• お問い合わせ

同一テーマ　記事一覧

• さらに見る