WEBマガジン

「＜Part 2＞人工知能技術の過去と現在（１）」

2018.06.15 株式会社オージス総研　　乾　昌弘

１．はじめに

（１）昨年度連載した「人工知能に関する内容」の「続編」として始めたいと思います。
（２）ディープラーニングをはじめとする機械学習は、非線形問題を扱っています。ここでは、「線形と非線形」という観点から「ニューラルネットワーク」「Genetic Algorithm」「数理計画法」を取り上げます。

２．線形と非線形

２－１．線形、非線形とは

（１）「線形」は、初期値が少し変わっても結果（解）は大きく変わらない。
　Y + dY = f ( X+dX)
　○比較的、解を得やすい。特徴がわかりやすい、理想的なかたちとして解く。

（２）「非線形」は、初期値が少し変われば結果は大きく変わる場合が多い。解を得るのに計算パワーが必要。全体像が捉えにくい（工夫すれば「捉えやすい」場合もある）
※「バタフライ効果」
James Gleickの著書 "Chaos: Making a New Science" では、「今日の北京で1匹の蝶が空気をかき混ぜれば、翌月のニューヨークの嵐が一変する」という形で説明されているようである。つまり、天気予報などは、スパコンを使ってやっと一週間程度の予測ができる。

２－２．最適化問題

（１）（私ごとですが）大学・大学院（機械系）6年間の前半は、数学を中心に流体力学、熱力学や機構学などを学び、後半は制御・システム工学を専攻。その中で最適化手法も学んだ。例えば、最大フロー最小カット定理、ダイナミックプログラミングである。
（２）最適化問題は結局、ある「制約条件」のもとで「評価関数（目的関数）」の最小値または最大値を求めることに帰する。

２－３．ニューラルネットワーク

（１）ニューラルネットワークなどの教師あり学習は、すべての「訓練データ」と「正解」との誤差が最小になるように決定する。（回帰分析のイメージ）
（２）中間層（隠れ層）がないニューラルネットワークの場合、
出力層の「ノード１」の出力Y1は（単純に考えると）
　　　Y1 = W1 + W11×X1 + W21×X2 +　...........　（X：入力層の出力、W：重み付け）で表される。
「正解」との誤差をXの値に比例して（＋－を考慮して）Wをδだけ修正する。これをすべての訓練データで繰り返す。

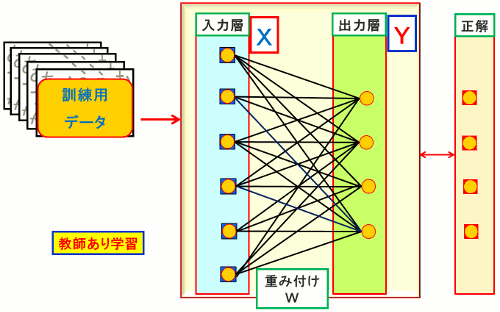
ニューラルネットワーク（中間層がない場合）果
図１．ニューラルネットワーク（中間層がない場合）

※Xの値に比例して修正するが、すべての誤差に対応するためにδだけ修正する。δが大きいと値が振動し、小さいと最適値になかなか近づかないという特徴がある。

（３）「中間層」がある場合は「非線形」となり、解くことが難しかったが、1986年Rumelhartが、3層以上のニューラルネットワークでBack Propagationにより、うまく学習できることを示した。
　（詳細は下記を参照）
　４．ニューラルネットワーク（Back Propagation）

３．Genetic Algorithm

３－１．Genetic Algorithm　とは、

（１）1990年代の初め、ニューラルネットワークと並んでブームになったのが、非線形な機械学習の1手法でもあるGenetic Algorithmである。「gene、crossover、mutation」がキーワードとなっている。
※カオス理論、フラクタルが流行ったのもこの頃です。

（２）現在でも最適化の一手法として使われているだけではなく、米国ではディープラーニングと並び、Genetic Algorithmが株取引などに使われている。

３－２．Genetic Algorithm　の概要

（１）0，1 を並べた列(genes)になっており、それぞれの意味づけを予め行う。
（２）ランダムで同じ意味づけの列を複数用意しておく。
　　※候補を多めに作成しておく。
（３）「訓練データ」と「正解」から、正解に近いものが生き残っていくように「crossover」を行う。
　　※有効なgenesが生き残っていく。

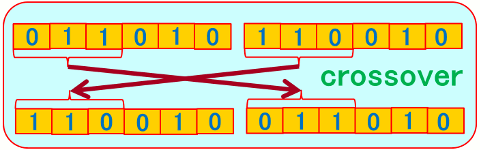
crossoverの方法
図２．crossoverの方法

（４）非線形特有の「極大値」あるいは「極小値」に近づかないように、２％程度のgenesの値を変更する（mutation）
（５） （３）（４）を繰り返して最適値に近づけていく。

mutationの方法
図３．mutationの方法

３－３．ニューラルネットワークとGenetic Algorithm

ニューラルネットワークは、ある程度基盤が出来上がっているのに対して、Genetic Algorithmは、Primitive（アセンブラ的）である。従って、実際の問題に適用するときに具体的な戦略が必要となる。
これは、人工知能言語であるPrologとLISPの関係に似ていると思う。

４．数理計画法

４－１．数理計画法とは、

（１）以前にも述べたが数理計画法などの最適化手法はかつて人工知能に含まれ、エキスパートシステムが経験的解法に対して論理的解法と呼ばれていました。
（２）図４のように「評価関数」は、ベクトルXの関数。「制約条件」は、Xが実行可能解の集合に含まれることである。
（３）「制約条件」には「ハード制約」と「ソフト制約」がある。ハード制約は、条件を満たさないと解にはならない。ソフト制約は優先順位である。

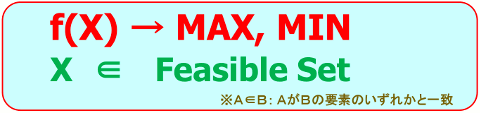
評価関数と制約条件
図４．評価関数と制約条件

４－２．線形計画法

線形計画法は高校２年数学の不等式で学習する。
※「線形計画法の文章題」（「参考文献」１より引用）
ある工場の製品にAとBの２種類がある。１kg生産するのに、Aは電力６０kwhとガス２立法m、Ｂは電力４０kwhとガス６立法mを要する。１kgあたりの価格は、Aは２万円、Bは３万円である。この工場への１日の供給量が電力２２００kwh、ガス１２０立法mまでとすると、１日に生産される製品の総価格を最大にするには、A、Bをそれぞれ何kgずつ生産すればよいか？

　評価関数：k＝20000x＋30000ｙ（最大値）
　制約条件：x、y＞＝0、60x＋40y＜＝2200、2x＋6y＜＝120

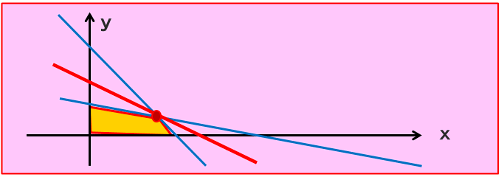
線形計画法の例
図５．線形計画法の例


※一般的には、Ｎ次元線形計画法となる。

４－３．ＭＩＰ（Mixed Integer Programming）など非線形計画

（１）ＭＩＰでは、例えば大型ポンプ1台が必要な場合と2台必要な場合とでは、電力量などが非常に違ってくる。（単純に考えると２倍）このような整数変数が含まれている。
（２）通常の問題は非線形の式を解く。すべて解くと、どこが最大値かわかるが、最初はまったくわからない（山に霧がかかった状態）解く方法には「メタヒューリスティックス法」などがある。場合によっては極大値を結論としてもよい。
（３）オープンソースやツールでは、いろいろな手法をメニューで選択できるようになっている。
※「メタヒューリスティックス法」：「ヒューリスティック」とは発見的方法という意味で、ある程度正しい解を導ける経験則。「メタ」で一段抽象化しており、特定の問題に関わらず一般的な解法という意味になる。代表的な解法としては、山登り法（最急降下法）がある。
「参考文献」
１．砂田利一編著「チャート式（赤チャート）数学Ⅱ」P142、数研出版（2004年4月）

「余談」
１．「行列」「統計」なども高校の数学で学習するので、統計解析や最適化の基礎は学んでいることになると思う。

*本Webマガジンの内容は執筆者個人の見解に基づいており、株式会社オージス総研およびさくら情報システム株式会社、株式会社宇部情報システムのいずれの見解を示すものでもありません。

『WEBマガジン』に関しては下記よりお気軽にお問い合わせください。

同一テーマ　記事一覧

「人工知能技術の過去と現在（最終回）」

2019.03.15 製造 株式会社オージス総研　　乾　昌弘

「＜Part 2＞人工知能技術の過去と現在（５）」

2018.11.12 製造 株式会社オージス総研　　乾　昌弘

「＜Part 2＞人工知能技術の過去と現在（４）」

2018.09.13 製造 株式会社オージス総研　　乾　昌弘

「＜Part 2＞人工知能技術の過去と現在（３）」

2018.08.10 製造 株式会社オージス総研　　乾　昌弘

＜Part 2＞人工知能技術の過去と現在（2）

2018.07.19 製造 株式会社オージス総研　　乾　昌弘

「人工知能技術の過去と現在（下）」

2018.03.19 製造 株式会社オージス総研　　乾　昌弘

「人工知能技術の過去と現在（上）」

2018.02.20 製造 株式会社オージス総研　　乾　昌弘

「スマートグリッド社会成熟度モデルと人工知能」

2018.01.24 製造 株式会社オージス総研　　乾　昌弘

「AIなどを通じて経験したGlobal Business」

2017.12.15 製造 株式会社オージス総研　　乾　昌弘

「ビジネスを解析する手法とその比較（AI含めて）」

2017.11.17 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（７）」

2017.10.25 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（６）」

2017.09.15 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（５）」

2017.08.28 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（４）」

2017.07.20 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（３）」

2017.06.19 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（２）」

2017.05.19 製造 株式会社オージス総研　　乾　昌弘

「＜オージス総研をとりまく＞人工知能技術の過去と現在（１）」

2017.04.17 製造 株式会社オージス総研　　乾　昌弘