WEBマガジン
「<Part 2>人工知能技術の過去と現在(4)」
2018.09.13 株式会社オージス総研 乾 昌弘
1.はじめに
※「CNN」は以下を参照のこと。
2.CNN(Convolutional Neural Network)
2.GAN(Generative Adversarial Network)(Reference-1)
2-1.GANとは、
(2)2014年、Ian J. Goodfellowが考え出した「教師なし学習」のモデルで、優れたアイデアとして脚光を浴びている。
※「教師なし学習」は以下も参考のこと。
3.「教師なし学習」ディープラーニング
2-2.GANの概要(図1参照)
● Generator(画像生成)、 Discriminator (分類)の2つのニューラルネットワーク(multilayer perceptrons)及び、X(真のデータ)で構成されている。
● Noise Z (ベクトル)をG (Generator)に入力すると画像 X'を出力。X'をD (Discriminator) に入力。
● D(Discriminator)はXとX'のそれぞれの結果を交互に出力、その結果を、DとGにフィードバックする。
●DはD (X)の出力が1(正解)に近づくように、またD (G (Z)) の出力が0(不正解)に近づくように学習する。一方、GはD (G (Z)) の出力が1(正解)に近づくように学習する。
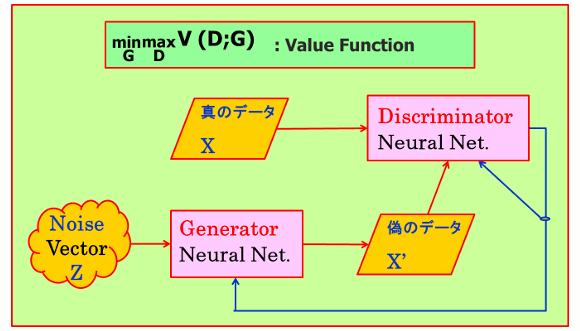
図1.GANの評価関数と概要図
論文にはそう書いてあり「なるほど」と思う反面、ゴールだけが決められ、ルールが厳密、詳細に決められていない点で、通常のゲームとは違う新しい面もあると思う。
(下記、論文より引用)
"In other words, D and G play the following two-player minimax game with value function"
2.ゲームの理論(基本)
偽札作りは本物に近いお札を作ろうとし、警察は本物と偽物を見分けようとします。お互いに学習し、警察の能力も上がるため、見破られないようにさらに巧妙な偽札を作ろうとします。こうして、本物と偽物の区別が付かない偽札ができるようになります。
(下記、論文より引用)
"The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency. Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles."
2-3.考察
(2)「この10年間で最もおもしろい機械学習」と言われている。
(3)訓練データが少ない場合に「GANにより足りないデータを補完」して機械学習させることができる。例えば、自動運転の開発ではいろいろなシーンに対する画像が必要であるが「GANが役に立つのではないか」と言われている。
※「機械学習」は以下も参照のこと
3.機械学習
※「自動運転」は以下を参照のこと
3.自動運転
「Reference」
1.Ian J. Goodfellow et al., "Generative Adversarial Nets", June 2014
3.Topology(位相幾何学)
3-1.経緯
(2)後に、大学院で知能ロボットの研究をしていた時「位相幾何学」が何か役に立たないか考えていましたが、思いつきませんでした。
(3)最近、形状認識を「ディープライニング」と「位相幾何学」を併用している場合があるようなので、紹介いたします。ただし、内容は忘却の彼方になっていますので、触りだけになると思います。
3-2.Topologyの特徴
(2)例えば大都市の地下鉄や高速道路は、距離そのものよりも何処が接続されているか(乗換駅、インターチェンジ)の方が重要になる場合が多い。
(3) 多少変形しても、縮んでも特徴が捉えられる
(4)重要なことは「画像や見える化されたデータ群の特徴」をルールや式で判別しょうとするときに「 Topologyが参考になる」と思い付くことです。特に詳細を知っている必要はなく、その時に調べればよいのです。
ということで紹介だけしておきます。
(5)人工知能の研究が (A) 人間の思考方法を解析して目指すか (B) プロセスはともかく結果的に人間の思考を模倣するか、の2つの方法があるとする。トポロジーは前者の様に思う。
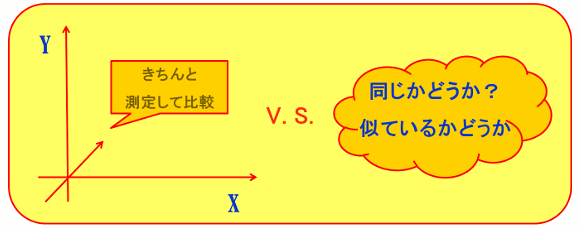
図2.ユークリッド幾何学とトポロジー
3-3.同相/異相
(2)よく使われる例でいくと (A) 「コーヒーカップとドーナツ」は同相 (B) 「取っ手のないコップと球」は同相です。しかし(C)これらのグループどうしは異相になります。
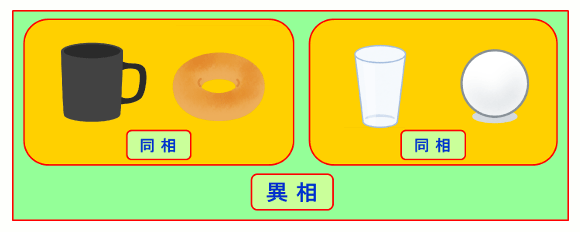
図3.「同相」対「異相」
3-4.オイラー標数
オイラーの標数=(頂点の数)-(辺の数)+(面の数)
結果は、すべて「2」になる。
(2)弾力のある多面体と考えて、膨らませると「球」になるのが「2」の条件と言われている。
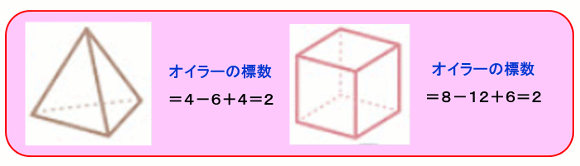
図4.オイラーの標数はすべて2(正多面体)
人工知能を考える上でも参考になると思います。
脳情報の意味空間では、脳内で「似たものとして表現されているものは近くに配置され、そうでないものは遠くに配置」されます。これにより、たとえばヒトに関係するカテゴリは脳内でクラスタとして表現されていることや、そのクラスタは動物に関係するクラスタと離れていること、しかしその間には体部位を示すクラスタが存在し、「集合として意味的な勾配」を形成しています。「CiNet News」脳情報通信融合研究センター(2017年4月14日発行)
*本Webマガジンの内容は執筆者個人の見解に基づいており、株式会社オージス総研およびさくら情報システム株式会社、株式会社宇部情報システムのいずれの見解を示すものでもありません。
『WEBマガジン』に関しては下記よりお気軽にお問い合わせください。
同一テーマ 記事一覧
 「人工知能技術の過去と現在(最終回)」
「人工知能技術の過去と現在(最終回)」
2019.03.15 製造 株式会社オージス総研 乾 昌弘
 「<Part 2>人工知能技術の過去と現在(5)」
「<Part 2>人工知能技術の過去と現在(5)」
2018.11.12 製造 株式会社オージス総研 乾 昌弘
 「<Part 2>人工知能技術の過去と現在(3)」
「<Part 2>人工知能技術の過去と現在(3)」
2018.08.10 製造 株式会社オージス総研 乾 昌弘
 <Part 2>人工知能技術の過去と現在(2)
<Part 2>人工知能技術の過去と現在(2)
2018.07.19 製造 株式会社オージス総研 乾 昌弘
 「<Part 2>人工知能技術の過去と現在(1)」
「<Part 2>人工知能技術の過去と現在(1)」
2018.06.15 製造 株式会社オージス総研 乾 昌弘
 「人工知能技術の過去と現在(下)」
「人工知能技術の過去と現在(下)」
2018.03.19 製造 株式会社オージス総研 乾 昌弘
 「人工知能技術の過去と現在(上)」
「人工知能技術の過去と現在(上)」
2018.02.20 製造 株式会社オージス総研 乾 昌弘
 「スマートグリッド社会成熟度モデルと人工知能」
「スマートグリッド社会成熟度モデルと人工知能」
2018.01.24 製造 株式会社オージス総研 乾 昌弘
 「AIなどを通じて経験したGlobal Business」
「AIなどを通じて経験したGlobal Business」
2017.12.15 製造 株式会社オージス総研 乾 昌弘
 「ビジネスを解析する手法とその比較(AI含めて)」
「ビジネスを解析する手法とその比較(AI含めて)」
2017.11.17 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(7)」
「<オージス総研をとりまく>人工知能技術の過去と現在(7)」
2017.10.25 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(6)」
「<オージス総研をとりまく>人工知能技術の過去と現在(6)」
2017.09.15 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(5)」
「<オージス総研をとりまく>人工知能技術の過去と現在(5)」
2017.08.28 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(4)」
「<オージス総研をとりまく>人工知能技術の過去と現在(4)」
2017.07.20 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(3)」
「<オージス総研をとりまく>人工知能技術の過去と現在(3)」
2017.06.19 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(2)」
「<オージス総研をとりまく>人工知能技術の過去と現在(2)」
2017.05.19 製造 株式会社オージス総研 乾 昌弘
 「<オージス総研をとりまく>人工知能技術の過去と現在(1)」
「<オージス総研をとりまく>人工知能技術の過去と現在(1)」
2017.04.17 製造 株式会社オージス総研 乾 昌弘
