第38回　「なんとなく」な意思決定の背後にある心理(1)－行動経済学と社会心理学②－

2013.09.10 山口 裕幸 先生

　経済学的あるいは確率論的には不可解な（間違っている）人間の意思決定が、当の人間にとっては極めて自然で合理的な決定である場合が多いことについて論じている。今回は、1990年以降、一般の人々のみならず、多数の数学の専門家を巻き込んで論議を呼んだモンティ・ホール問題（Monty Hall problem）を題材にして考えてみたい。モンティ・ホールは、アメリカのクイズテレビ番組の司会者であり、彼の出した問題が事の発端である。その問題とは次のようなものであった。

　あるテレビ番組で勝利者となったあなたは、非常に魅力的な賞品をもらえるチャンスを得た。今、A、B、C３つのドアがあって、そのどれか１つの向こう側に賞品が置かれている。残り２つのドアはハズレである。あなたはどれか１つのドアを選び、そのドアを開いて賞品が置かれていればアタリ！というわけである。あなたはAを選んだとしよう。すると、番組の司会者が「あなたが選んだAのドアをあける前に、残りのBとCはハズレであるか確かめましょう」といって、BとCのどちらかをあけることにした。そして、Cのドアをあけたところハズレであった。残るはAとBの２つである。ここで司会者が「あなたはAを選んでいますが、今なら、Bに変えることができます。Aのままで行きますか、それともBに変えますか」と尋ねてきた。あなたなら、どう判断するだろうか。選択を変えた方が当たるのだろうか、変えない方があたるのだろうか。

　まず誰もが思うのは、最初にどのドアを選んでも、当たる確率はどれも１／３だということである。「どれでも同じだけどなあ」と思いつつ、選ぶことになる。次に、Cはハズレであると判明した後に考えることは、「AかBかどちらかなのだから、当たる確率は１／２ずつだ」ということだろう。しかし、ここに落とし穴がある。当たる確率は、最初の段階で決まっていて、あなたが選択したAのドアが当たりである確率は１／３で、このことは誰もが承知のことである。ただ、この事実は、BあるいはCが当たりである確率は２／３であることも意味している。この確率は、Cがハズレであることが分かった後も変わりがない。むしろ、BあるいはCが当たりである確率は２／３のままである中で、Cがハズレであることがわかったのだから、残されたBが当たりである確率が２／３ということになる。Aが当たりである確率は相変わらず１／３のままであり、Bが当たりである確率はCの選択肢が排除できたおかげで２／３である。したがって、選択を変えた方が当たる確率は２倍も大きくなることになる。

　モンティ・ホール問題に対して、アメリカのコラムニストであるサヴァント(Marilyn vos Savant)が、雑誌Paradeの彼女のコラム欄「マリリンに聞く」の中で、「正解は『変更する』である。なぜなら、ドアを変更した場合には、当たる確率が変更しない場合の2倍になるからだと」書いたところ、膨大な数の否定と批判の意見が寄せられる事態となった。その批判者の中には、高名な数学者エルデシュ（Paul Erds）をはじめとして、数多くの権威ある研究者が名を連ねている。確率論的には上述の説明の通りであるし、コンピュータ・シミュレーションでもサヴァントの回答が正しいことが実証されている。面白いのは、なぜ優れた数学者でさえも「選択を変えても、変えなくても同じこと」と思ってしまったかという点だ。

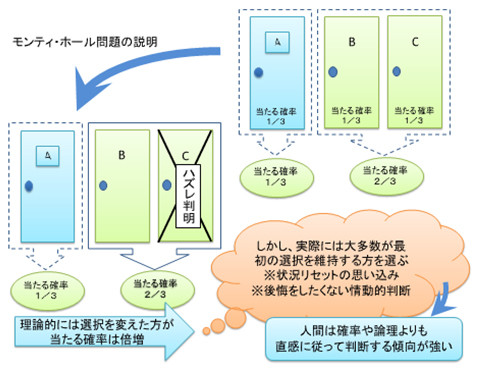
　もし、Cのハズレが判明した後、残った２つのドアの向こう側の賞品とハズレの置き方を再度やり直したとしたら、当たりの確率はリセットされて１／２ずつになる。しかし、そんなやり直しは行われていない。当たる確率は最初の段階で決まっていて変化がないのに、Cがハズレであることが判明したことで、我々は状況をリセットして判断してしまい、ついつい残った２つの選択肢が対等な当選確率になったと思ってしまう。この直感的なリセットはかなり根強く、どんなに確率的に説明しても納得できない人が多いため、論議は拡大し、モンティ・ホール問題は、パラドックス課題であるとか、ディレンマ課題とか称されることさえある。しかし、本質的には、人間の直感が確率論に基づいた理論的な思考とは乖離してしまうことが、理解を難しくさせている理由の根底にある。

　また、状況認識を勝手にリセットしてしまうことに加えて、人間の情動的な要因もこの問題の理解を難しくしていることも指摘しておきたい。大学の講義中に、実際に学生たちにこの課題を与えて判断を求める実験を行ってみると、Aの選択を維持して変えないという人が8割以上にのぼり、圧倒的に多い。理由を尋ねると、「選択を変えてハズレだったら、そのままにしておけば当たりだったのにとひどく後悔しそうだから」とか「初志貫徹した方がいいような気がするから」といった答えが多く見られた。前回紹介したプロスペクト理論からもわかるように、我々は、損失（マイナス）が生じることには敏感で、できればそれを避けようとする直感的な判断が働いてしまうものなのである。モンティ・ホール問題でも、変えた場合に見込まれる利得と損失を天秤にかけて、当たる確率は同じだと思ってしまったら、次にはハズレたときのダメージを先に考えてしまうのである。モンティ・ホール問題は、人間の持つ直感の特性が二重に働いて、正解の理解を困難にしていると言えそうだ。

　今回紹介した事例は、人間が「認知的節約家(cognitive miser)」であることに由来する直感が働く場合についてのものである。論理的に見たときに不可解に写る人間の意思決定の特性については、まだいくつかの側面がある。次回は、また違った側面から、人間の意思決定が、理論的正解とは乖離したものになりがちな理由について考えていくことにしたい。

※先生のご所属は執筆当時のものです。

関連記事一覧